Предмет: Алгебра,
автор: Elizabetsimmer
ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА
Приложения:
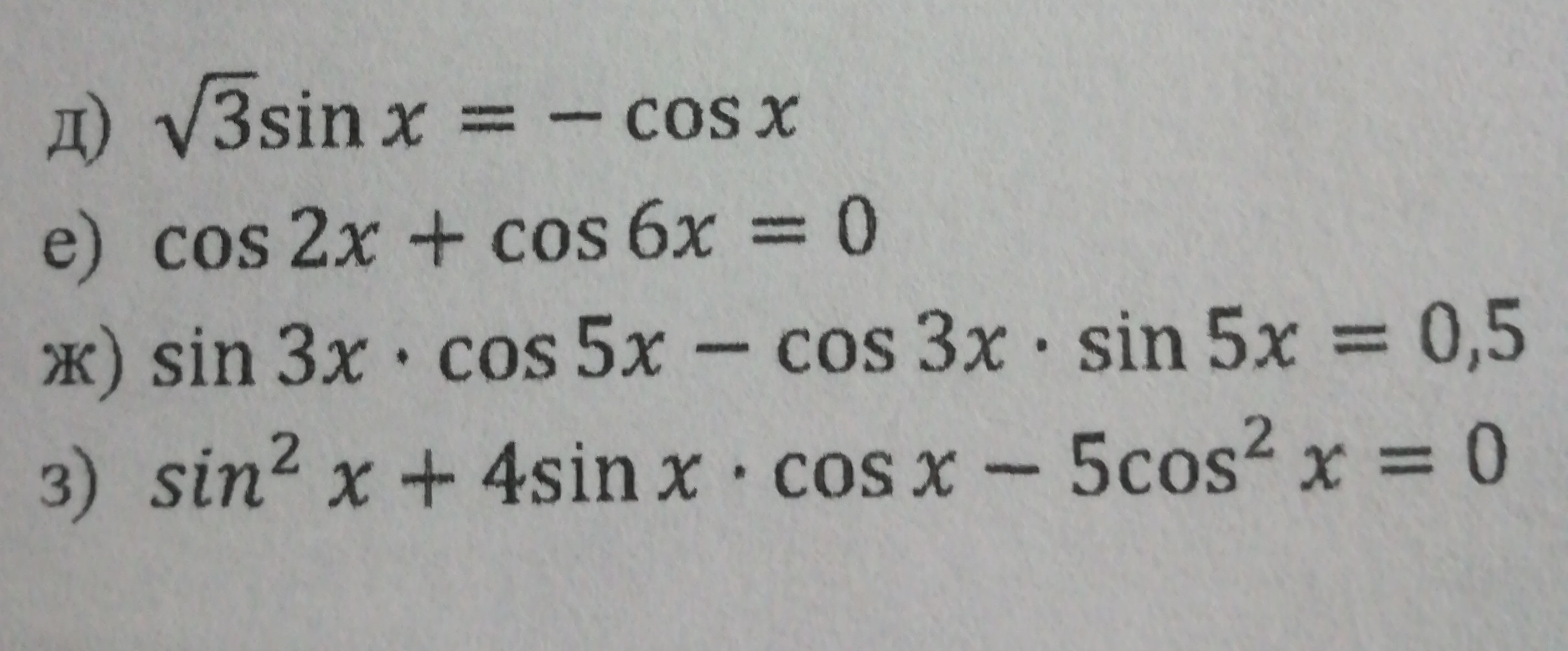
Ответы
Автор ответа:
1
Elizabetsimmer:
БЛАГОДАРЮЮЮ
Похожие вопросы
Предмет: Геометрия,
автор: Yulia23632
Предмет: Литература,
автор: nastyaa156
Предмет: Геометрия,
автор: Yulia23632
Предмет: Алгебра,
автор: khrabanly