Предмет: Алгебра,
автор: korchevnaya2016
Вычислить интеграл. Срочно. Даю 30 баллов
Приложения:
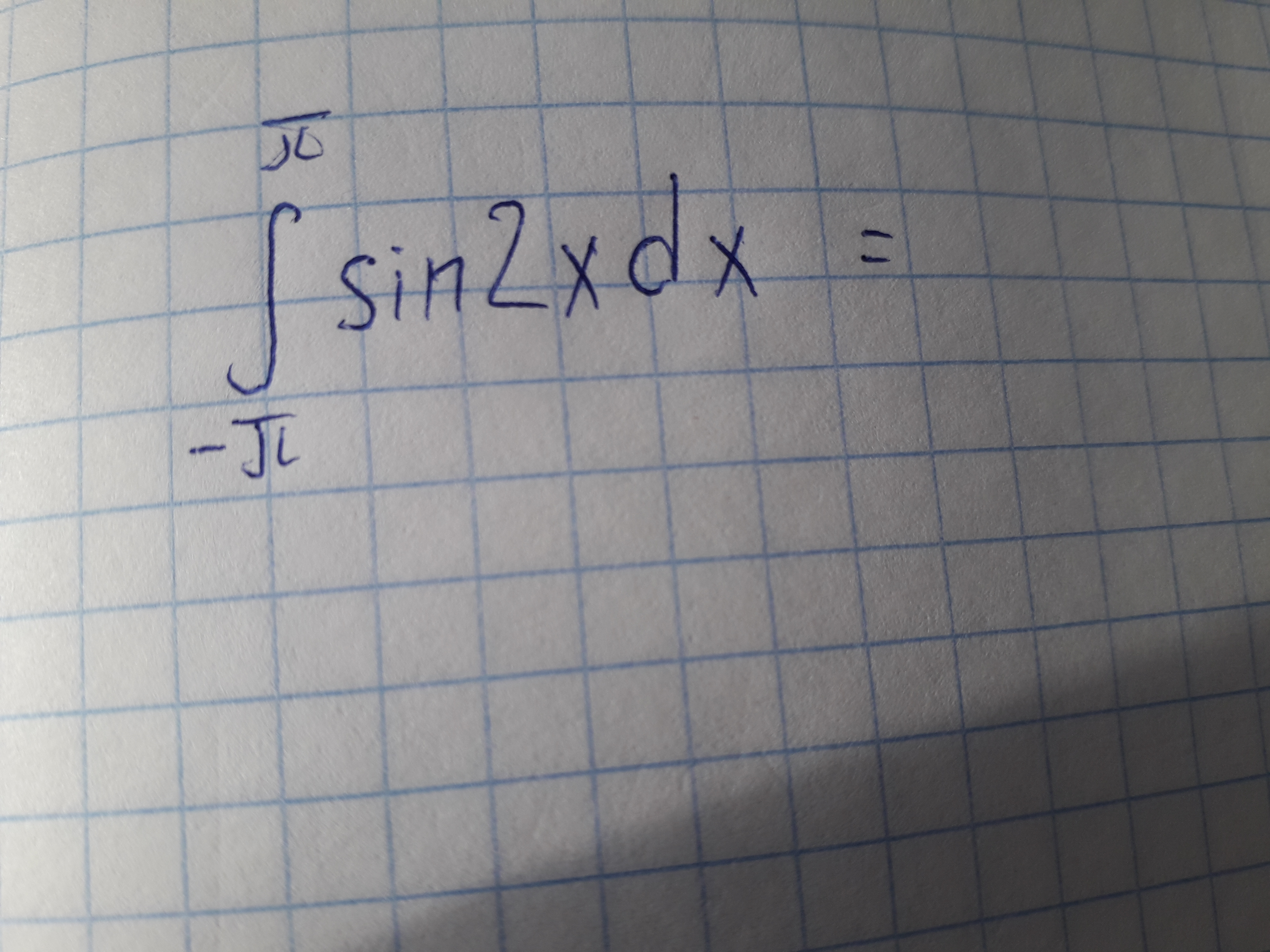
Ответы
Автор ответа:
1
Чтобы подынтегральное выражение совпадало с табличным интегралом от синуса, мы двойку занесли под дифференциал, одновременно разделив на 2. Действительно, d(2x) = 2dx. Зато переменная интегрирования стала совпадать с переменной синуса.
Затем по формуле Ньютона-Лейбница вычислем определённый интеграл.
korchevnaya2016:
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: olgapasinchuk1256
Предмет: Математика,
автор: lalalalala00000
Предмет: Алгебра,
автор: BigMuhammadali
Предмет: Биология,
автор: МайяБрусиловская
Предмет: География,
автор: mistergloz