Предмет: Алгебра,
автор: donik06
Помогите решить 1 и 4.Буду благодарен.
Приложения:
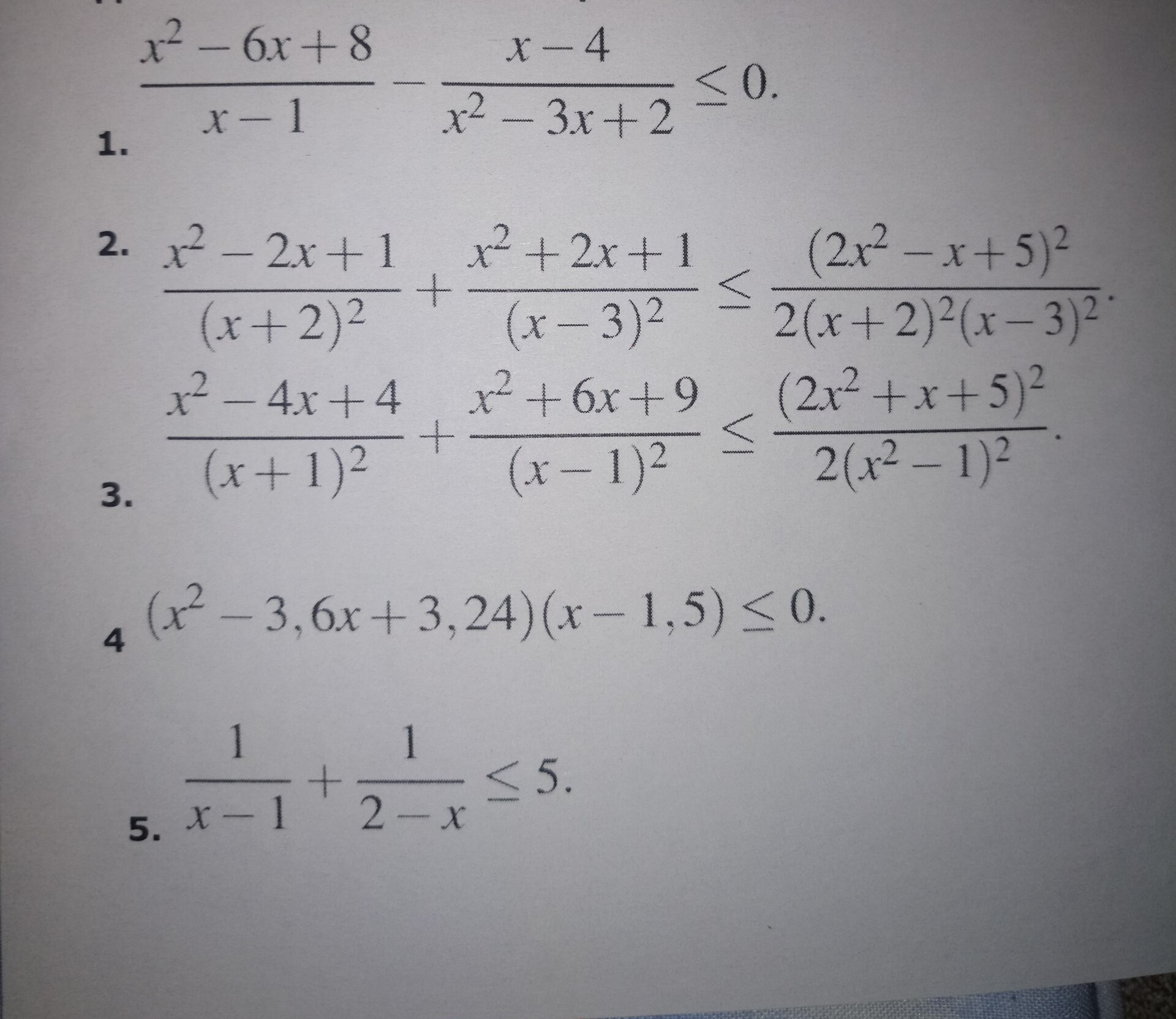
Ответы
Автор ответа:
2
задание решено 
Приложения:
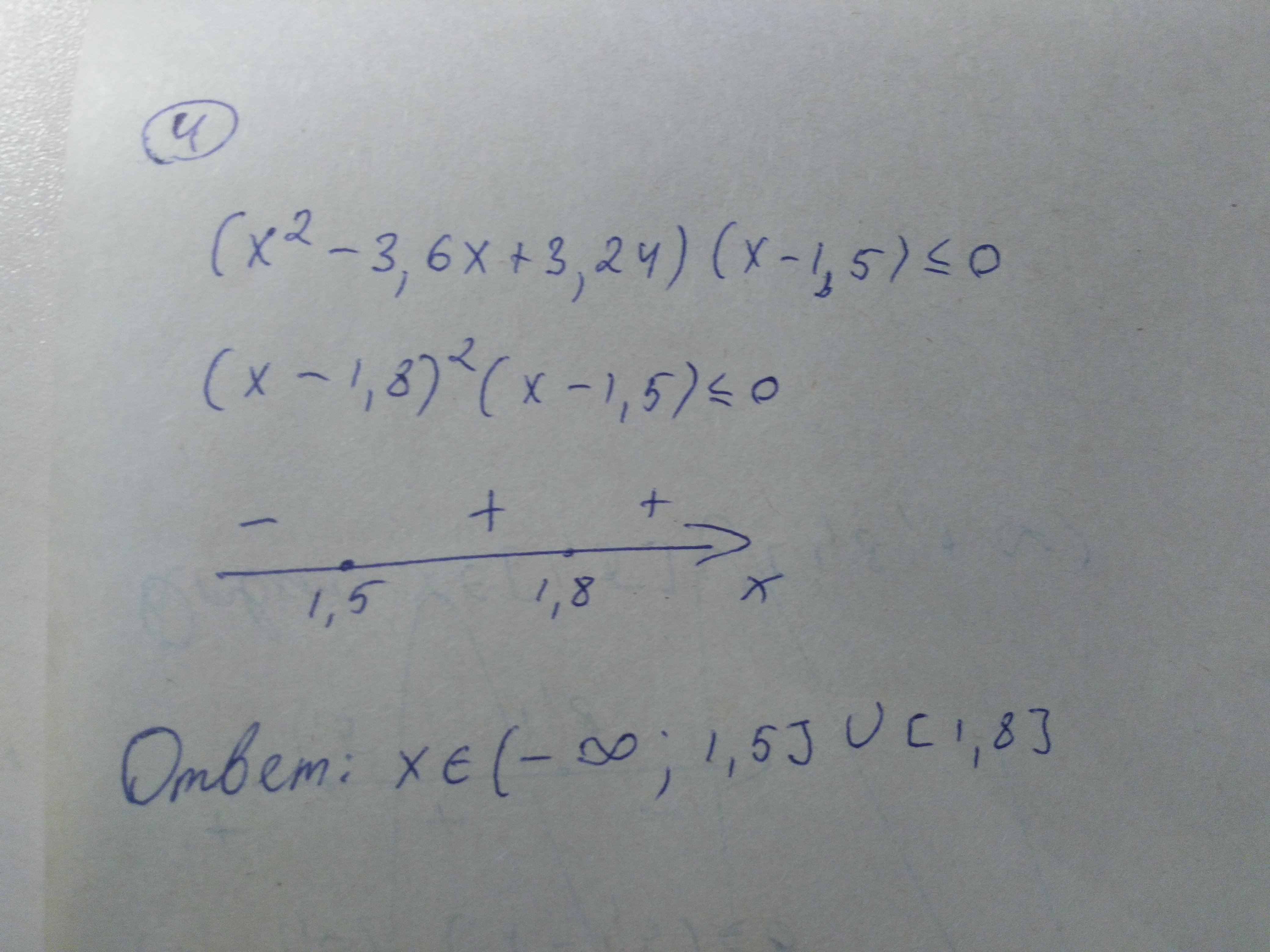
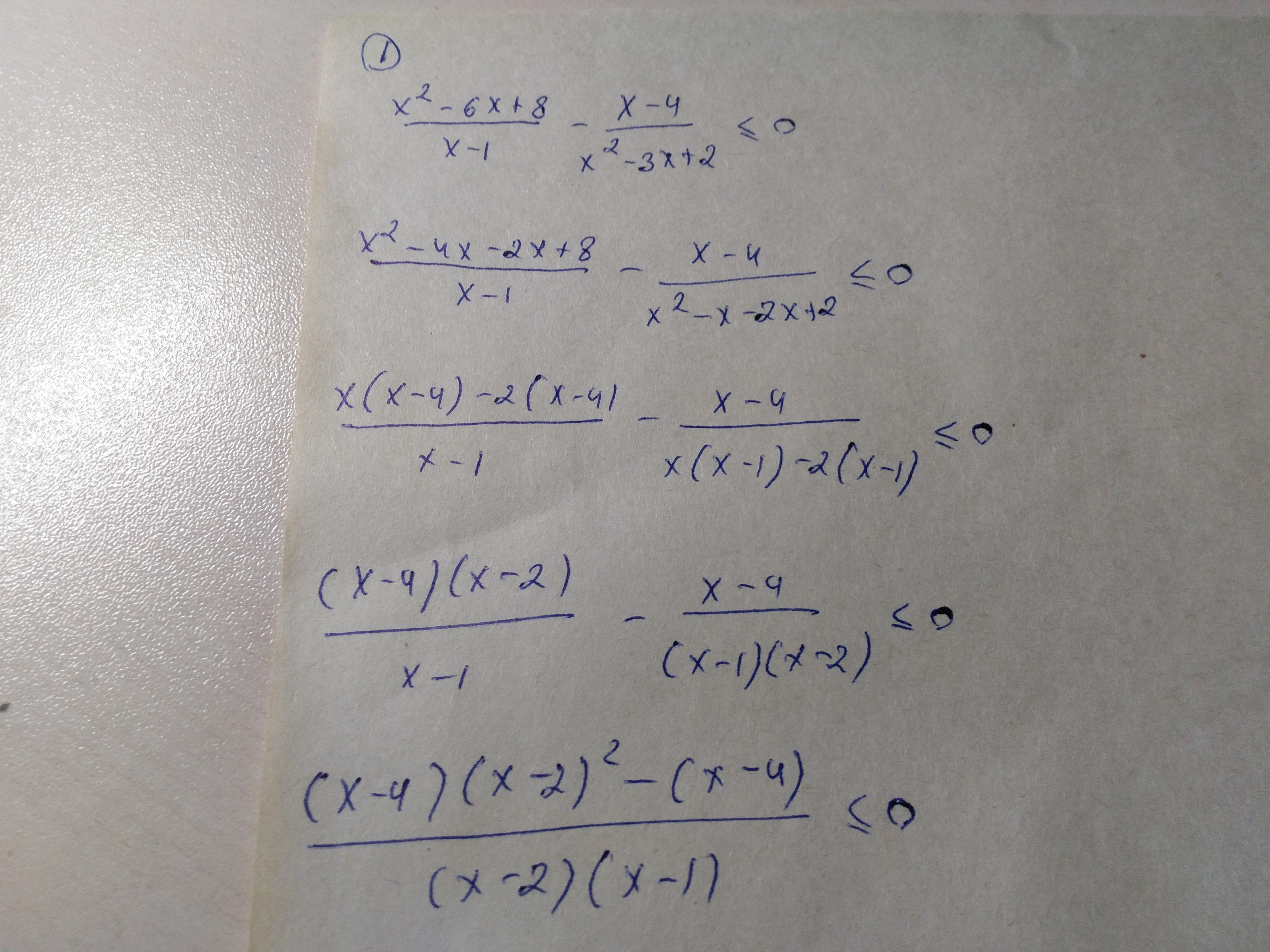
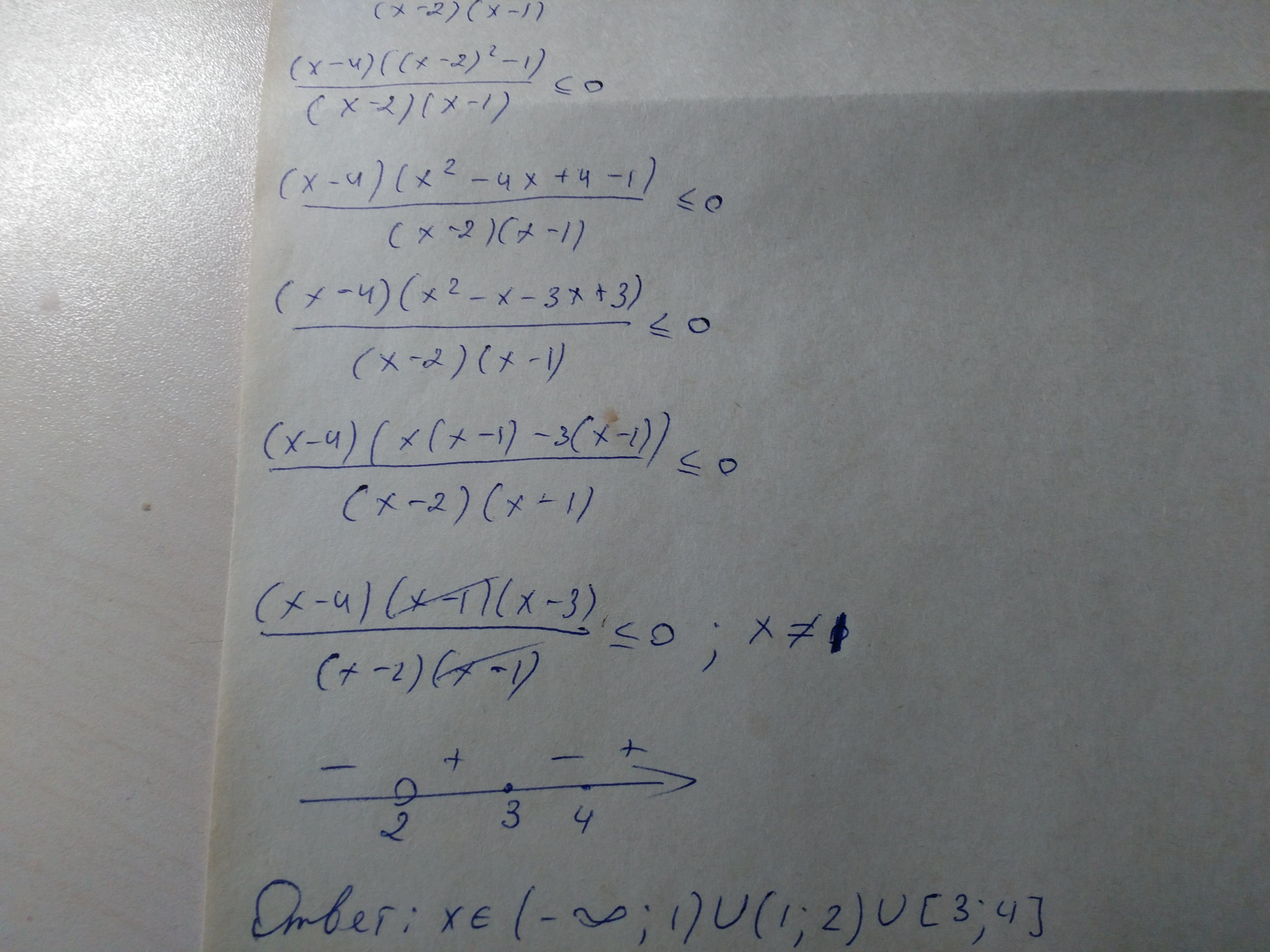
Автор ответа:
0
1
x²-6x+8=0
x1+x2=6 U x1*x2=8⇒x1=2 U x2=4
x²-3x+2=0
x1+x2=3 U x1*x2=2⇒⇒x1=1 U x2=2
(x-2)(x-4)/(x-1)-(x-4)/(x-1)(x-2)≤0
[(x-4)(x-2)²-(x-4)]/(x-1)(x-2)≤0
(x-4)(x²-4x+4-1)/(x-1)(x-2)≤0
(x-4)(x²-4x+3)/(x-2)(x-1)≤0
x²-4x+3=0
x1+x2=4 U x1*x2=3⇒x=1 U x=3
(x-4)(x-1)(x-3)/(x-1)(x-2)≤0
(x-4)(x-3)/(x-2)≤0,x≠1
_ _ + _ +
------(1)-----------(2)-------------[3]-----------[4]-------
x∈(-∞;1) U (1;2) U [3;4]
4
(x-1,8)²(x-1,5)≤0
_ + +
--------[1,5]-------------[1,8]------------
x∈(-∞;1,5] U {1,8}
x²-6x+8=0
x1+x2=6 U x1*x2=8⇒x1=2 U x2=4
x²-3x+2=0
x1+x2=3 U x1*x2=2⇒⇒x1=1 U x2=2
(x-2)(x-4)/(x-1)-(x-4)/(x-1)(x-2)≤0
[(x-4)(x-2)²-(x-4)]/(x-1)(x-2)≤0
(x-4)(x²-4x+4-1)/(x-1)(x-2)≤0
(x-4)(x²-4x+3)/(x-2)(x-1)≤0
x²-4x+3=0
x1+x2=4 U x1*x2=3⇒x=1 U x=3
(x-4)(x-1)(x-3)/(x-1)(x-2)≤0
(x-4)(x-3)/(x-2)≤0,x≠1
_ _ + _ +
------(1)-----------(2)-------------[3]-----------[4]-------
x∈(-∞;1) U (1;2) U [3;4]
4
(x-1,8)²(x-1,5)≤0
_ + +
--------[1,5]-------------[1,8]------------
x∈(-∞;1,5] U {1,8}
Похожие вопросы
Предмет: Математика,
автор: lohvita584
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: rylenx
Предмет: Математика,
автор: АлмазДоширак
Предмет: Биология,
автор: dfsdfsdjkjskdhf