Question

1. Какое из следующих утверждений неверно?
а) Если прямая перпендикулярна к двум прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости;
б) если прямая перпендикулярна к плоскости, то она ее пересекает;
в) если две плоскости перпендикулярны к прямой, то они параллельны;
г) если две прямые перпендикулярны к плоскости ,то они параллельны.
2. Две наклонные, проведенные к плоскости, имеют равные проекции. Равны ли сами наклонные?
3. Если одна из двух скрещивающихся прямых перпендикулярна к плоскости, то будет ли перпендикулярна к этой плоскости вторая прямая?
а) Да; б) да, но при определенных условиях; в) определить нельзя; г) нет.
4. Точка E не принадлежит плоскости прямоугольника ABCD. BE⊥ AB, BE⊥ BC. Тогда прямая CD и плоскость BCE:
а) параллельны; б) перпендикулярны; в) определить их взаимное расположение нельзя ; г) прямая лежит в плоскости.
5. АВСД – квадрат. Вне его плоскости выбрана точка К, причем КА ⊥ АВ. Плоскости АКД перпендикулярна прямая
а) ДС; б) КС; в) ВК; г) ВС.

Answer 1

1.

а) Пропущено слово "пересекающимся" - неверно!

б) Верно, если не пересекает, то параллельна

в) Ну вообще-то еще они могут и совпадать... - неверно!

г) Верно

2.

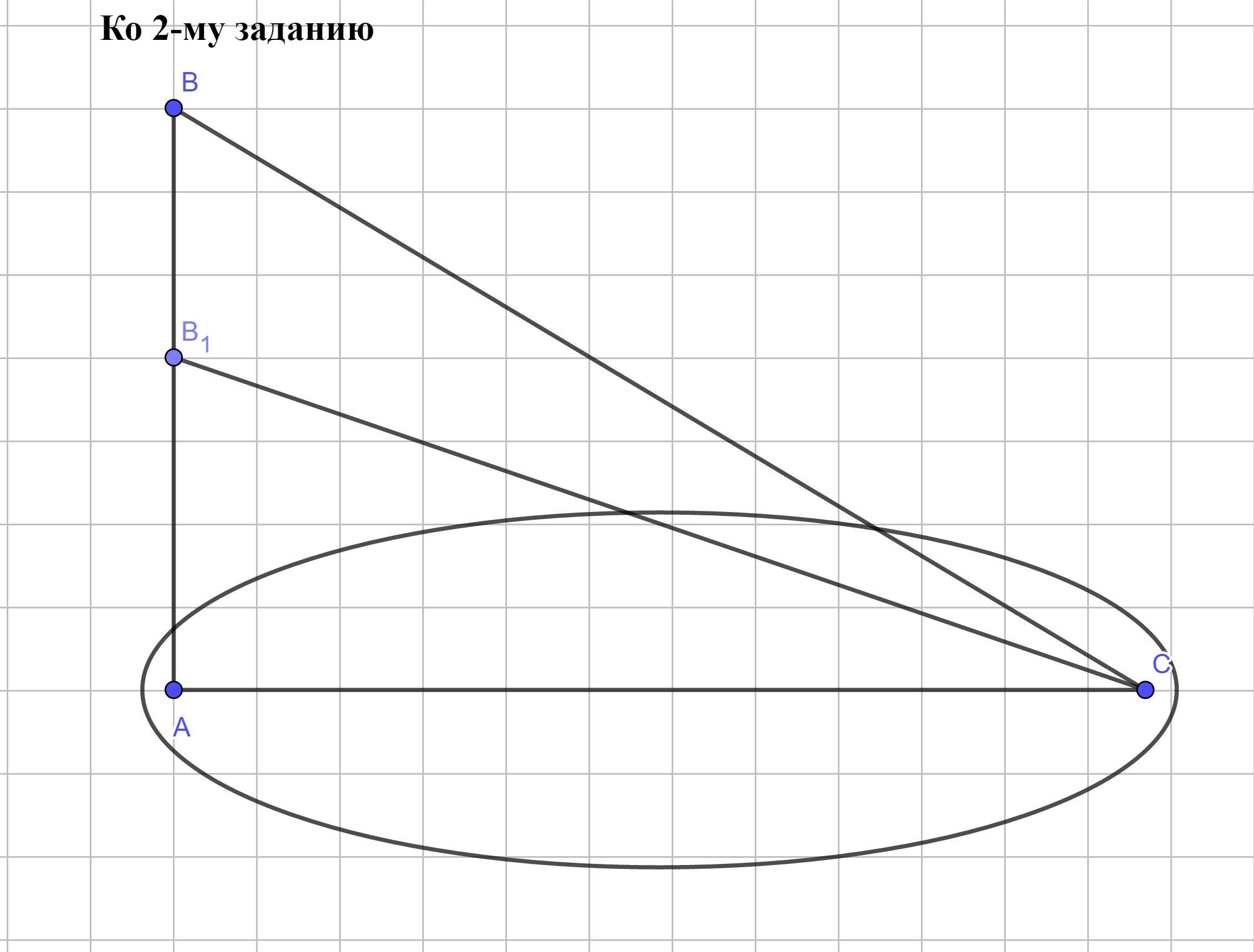
Нет! Взяв разные точки на перпендикуляре к плоскости, и соединив их с любой точкой плоскости (отличной от основания перпендикуляра) получим разные наклонные с общей проекцией (см. 1-й рисунок - наклонные CB₁ ≠ CB имеют общую проекцию AC).

3.

Если бы ответ был "да" - получили бы противоречие с тем, что прямые скрещиваются (они были бы параллельны!) Ответ: нет

4.

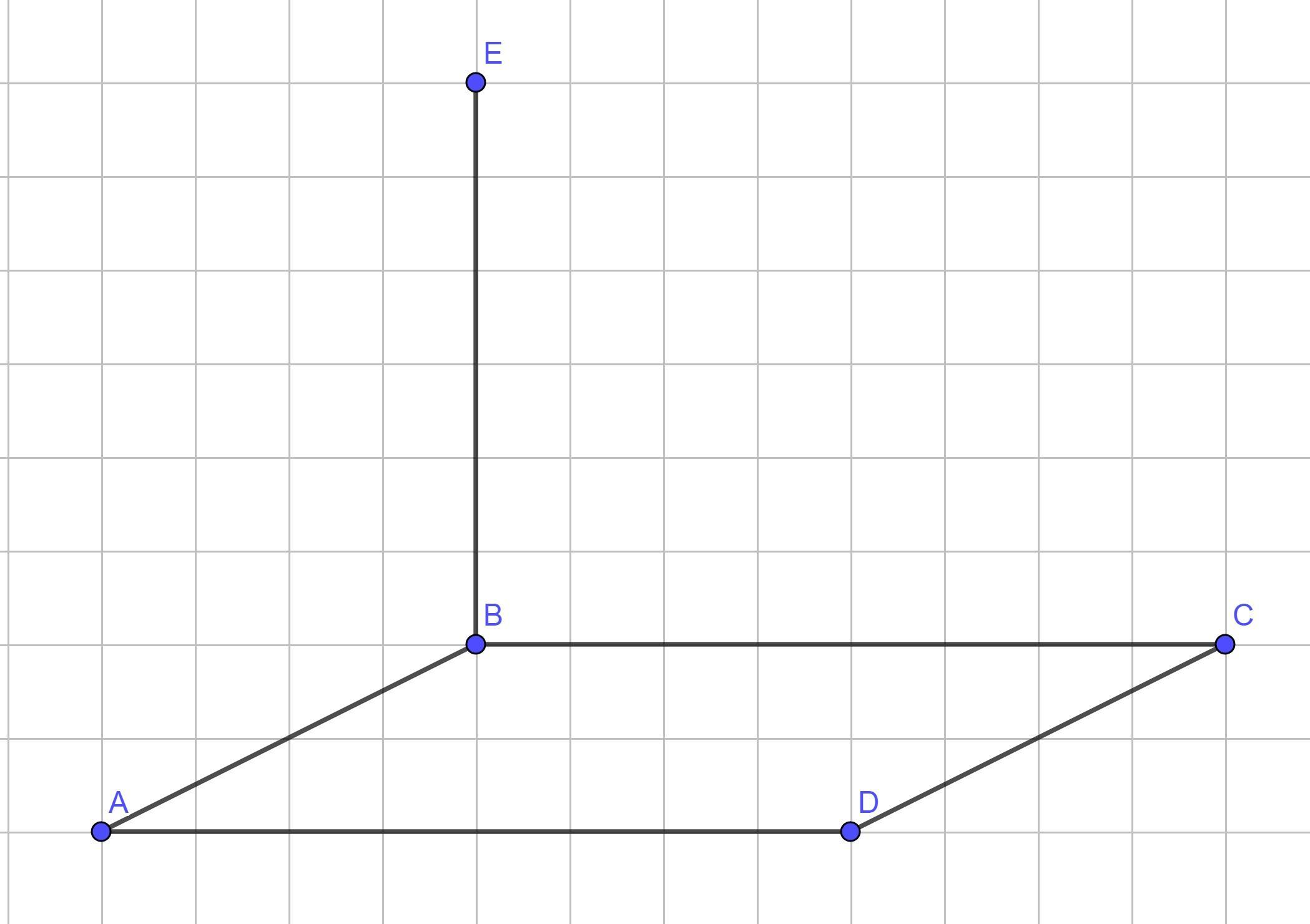
BE ⊥ пл. (ABC) по признаку (по условию) ⇒ перпендикулярна любой прямой, лежащей в этой плоскости. Получаем BE ⊥ CD и BC ⊥ CD (по условию) ⇒ CD ⊥ (BCE) (см 2-й рисунок) Правильный ответ б)

5.

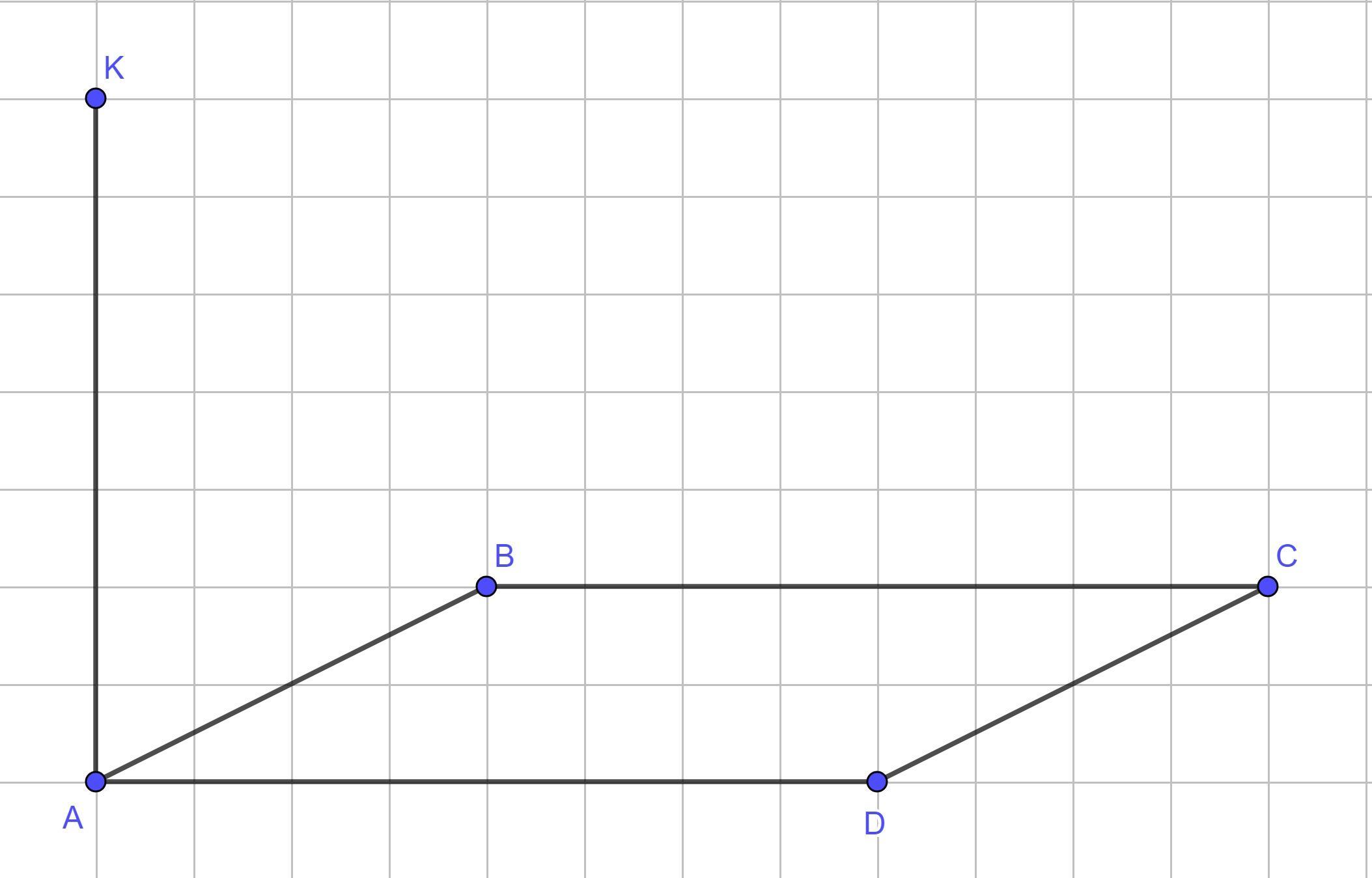
KA ⊥ AB (по условию), AD ⊥ AB ( по условию) ⇒ AB ⊥ пл. (AKD) - по признаку; CD ║ AB ⇒ CD ⊥ пл. (AKD) (см 3-й рисунок) Правильный ответ а)