Предмет: Геометрия,
автор: Liza123Kravchenko
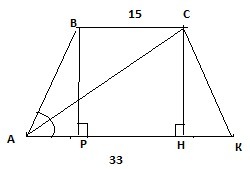
Основания равнобедренной трапеции равны 15 и 33 см, диагональ делит её острый угол пополам. Найти площадь трапеции.
Ответы
Автор ответа:
4
По свойству трапеции ВС║АК⇒
∡САК=∡АСВ как накрест лежащие, по условию ∡САК=∡ВАС, так как АС-биссектриса ∡А по условию.⇒∡ВАС=∡ВСА и ΔАВС-равнобедренный, значит АВ=ВС=15см.
Опустим ВР и СН-высоты, тогда АР=НК=(33-15)/2=9см.
По теореме Пифагора ВР=√(АВ²-АР²)=√(225-81)=12см.
S=ВР*(ВС+АК)/2=12*48/2=288см².
∡САК=∡АСВ как накрест лежащие, по условию ∡САК=∡ВАС, так как АС-биссектриса ∡А по условию.⇒∡ВАС=∡ВСА и ΔАВС-равнобедренный, значит АВ=ВС=15см.
Опустим ВР и СН-высоты, тогда АР=НК=(33-15)/2=9см.
По теореме Пифагора ВР=√(АВ²-АР²)=√(225-81)=12см.
S=ВР*(ВС+АК)/2=12*48/2=288см².
Приложения:
Похожие вопросы
Предмет: Литература,
автор: gggggggggggggg4018
Предмет: Литература,
автор: leviakk838
Предмет: Физика,
автор: sharovarskiisergey
Предмет: История,
автор: Zima111
Предмет: Математика,
автор: diana22072004