Предмет: Геометрия,
автор: Ana442
ПОМОГИТЕ,ДАЮ 25 БАЛЛОВ
3 и 4
Приложения:

Ответы
Автор ответа:
1
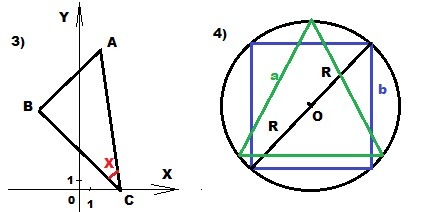
3) Найдите косинус угла С треугольника ABC, если А(2;14), В(-4;8), С(4;0)
Длина отрезков по формуле расстояния между точками



Теорема косинусов
AB² = AC²+CB² - 2AC*CB*cos∠ACB
72 = 200 + 128 - 2*10√2 * 8√2 * cos∠ACB
320·cos∠ACB = 256
cos∠ACB = 256/320 = 4/5 = 0,8
4) В окружность вписаны равносторонний треугольник (P = 90 см) и квадрат. Найти Р квадрата
Сторона равностороннего треугольника
a = Р/3 = 90/3 = 30 см
Радиус окружности, описанной около треугольника
R = a/√3 = 30/√3 =10√3 см
Диаметр окружности = диагонали квадрата
D = 2R = 2*10√3 = 20√3 см
Сторона квадрата (можно по теореме Пифагора)
b = D/√2 = 20√3/√2 =10√6 см
Периметр квадрата
P = 4b = 40√6 см
Длина отрезков по формуле расстояния между точками
Теорема косинусов
AB² = AC²+CB² - 2AC*CB*cos∠ACB
72 = 200 + 128 - 2*10√2 * 8√2 * cos∠ACB
320·cos∠ACB = 256
cos∠ACB = 256/320 = 4/5 = 0,8
4) В окружность вписаны равносторонний треугольник (P = 90 см) и квадрат. Найти Р квадрата
Сторона равностороннего треугольника
a = Р/3 = 90/3 = 30 см
Радиус окружности, описанной около треугольника
R = a/√3 = 30/√3 =10√3 см
Диаметр окружности = диагонали квадрата
D = 2R = 2*10√3 = 20√3 см
Сторона квадрата (можно по теореме Пифагора)
b = D/√2 = 20√3/√2 =10√6 см
Периметр квадрата
P = 4b = 40√6 см
Приложения:
Ana442:
больше спасибо!!!
Похожие вопросы
Предмет: Русский язык,
автор: alyadashevskaya
Предмет: Геометрия,
автор: edobaliev
Предмет: Химия,
автор: olgaromanyk21
Предмет: Математика,
автор: sefserj
Предмет: Алгебра,
автор: Ar4yy27