Предмет: Алгебра,
автор: avokebest
Найти неопределённый интеграл подробно , со всеми пояснениями. Результаты проверить дифференцированием
Приложения:
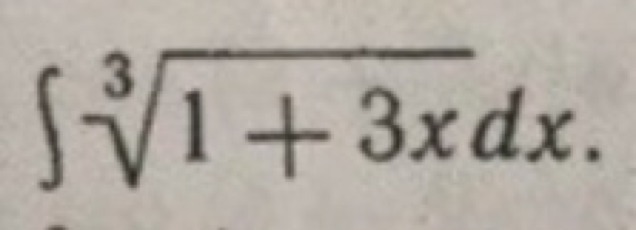
Ответы
Автор ответа:
0
Проверка:
Похожие вопросы
Предмет: Другие предметы,
автор: ila221332
Предмет: История,
автор: paskozena294
Предмет: Физика,
автор: sharandakkata
Предмет: Алгебра,
автор: valentin3105199
Предмет: Математика,
автор: Qouris