Предмет: Математика,
автор: djputinnp29xmb
Помогите: где я ошибся в задаче по геометрии?
Угол между диаметром АВ и хордой АС равен 30°. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник ACD равнобедренный.
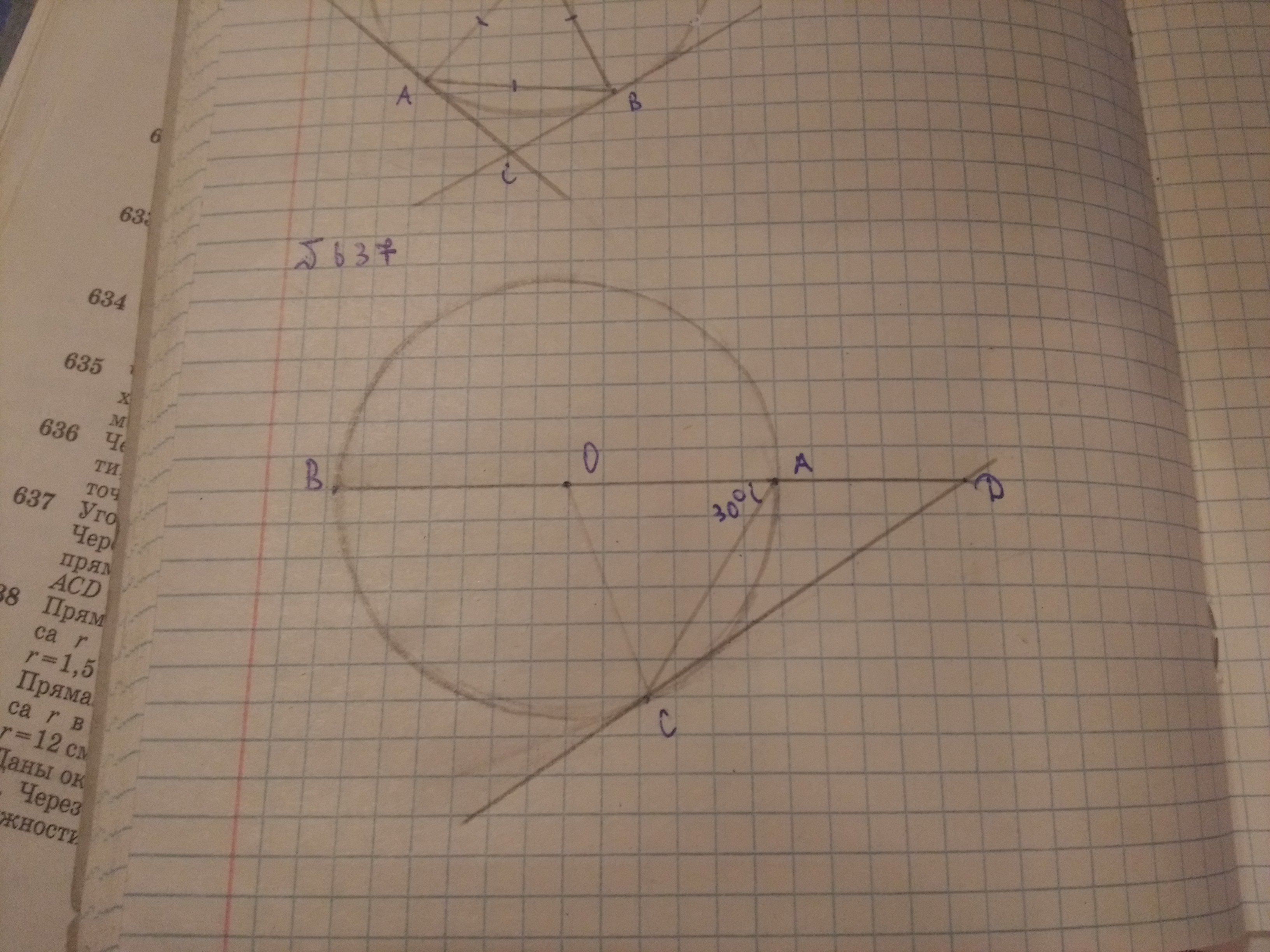
У меня получается, что сумма углов треугольника ACD > 180 градусов. Где я ошибся в чертеже?
Приложения:
безумец01:
180-30=150 ,,180-150=30 ,,30/2=15 ,,углы с и д по 15 градусов,если асд равнобедренный
Так нужно доказать что он равнобедренный. У меня получается, что OA = OC ==> угол OCA = 30гр.; угол ACD = 90гр. - OCA = 60гр.; угол CAD = 180 - 30 = 150 гр. уже больше 180 гр. в треугольнике ACD
угол осд =90 градусов, касательная к радиусу 90 градусов
углы с и д в треугольнике асд равны между собой ,а значит и равнобедренный,,,задача на построение или на вычисление
Ответы
Автор ответа:
2
Из ΔАОС:
ОС = ОА (радиусы) ⇒ ΔАОС - равнобедренный ⇒ ∠ОСА = 30°
∠АОС = 180 - (∠ОАС + ∠ОСА) = 180 - (30+30) = 120°
Из ΔСОD:
∠DOC = 180 - ∠АОС = 180 - 120 = 60° (смежные углы)
∠ОСD = 90° (радиус, проведенный в точку касания ⊥ касательной)
∠ОDC = 90 - ∠DOC = 90 - 60 = 30°
∠ОDC = ∠ОАС = 30° ⇒ ΔACD - равнобедренный
ОС = ОА (радиусы) ⇒ ΔАОС - равнобедренный ⇒ ∠ОСА = 30°
∠АОС = 180 - (∠ОАС + ∠ОСА) = 180 - (30+30) = 120°
Из ΔСОD:
∠DOC = 180 - ∠АОС = 180 - 120 = 60° (смежные углы)
∠ОСD = 90° (радиус, проведенный в точку касания ⊥ касательной)
∠ОDC = 90 - ∠DOC = 90 - 60 = 30°
∠ОDC = ∠ОАС = 30° ⇒ ΔACD - равнобедренный
Приложения:

Я уже решил её по такому чертежу. Просто, я не могу понять: что в моём исходном чертеже неверно?
на вашем рисунке треугольник АОС остроугольный, а должен быть тупоугольным, отсюда ошибка в построении и путаница в решении.
Спасибо.
пожалуйста
какая разница между тем построением и этим ,что там что здесь равнобедренный треугольник
разница в расположении точки Д. Эта точка не может быть расположена справа от окружности потому что треугольник АОС тупоугольный.
угол аос заранее не оговаривался при задании
и что? от этого он не стал острым. Если сумма углов треугольника = 180 и треугольник АОС имеет 2 угла по 30 градусов, то чему равен третий угол этого треугольника? Есть вариант, при котором этот угол может быть острым?
у него просто перемешались треугольники аос и асд и он запутался,,хотя задача имеет 2 варианта решения
Задача имеет единственное решение. Не путайте задавшего вопрос еще больше.
Похожие вопросы
Предмет: Английский язык,
автор: olgabanikevich
Предмет: Химия,
автор: zlatasamojlenko5
Предмет: Алгебра,
автор: sfswmyn897
Предмет: Математика,
автор: khayrullaev1986