Предмет: Математика,
автор: sara131
Решите уравнение логорифмическое
Приложения:
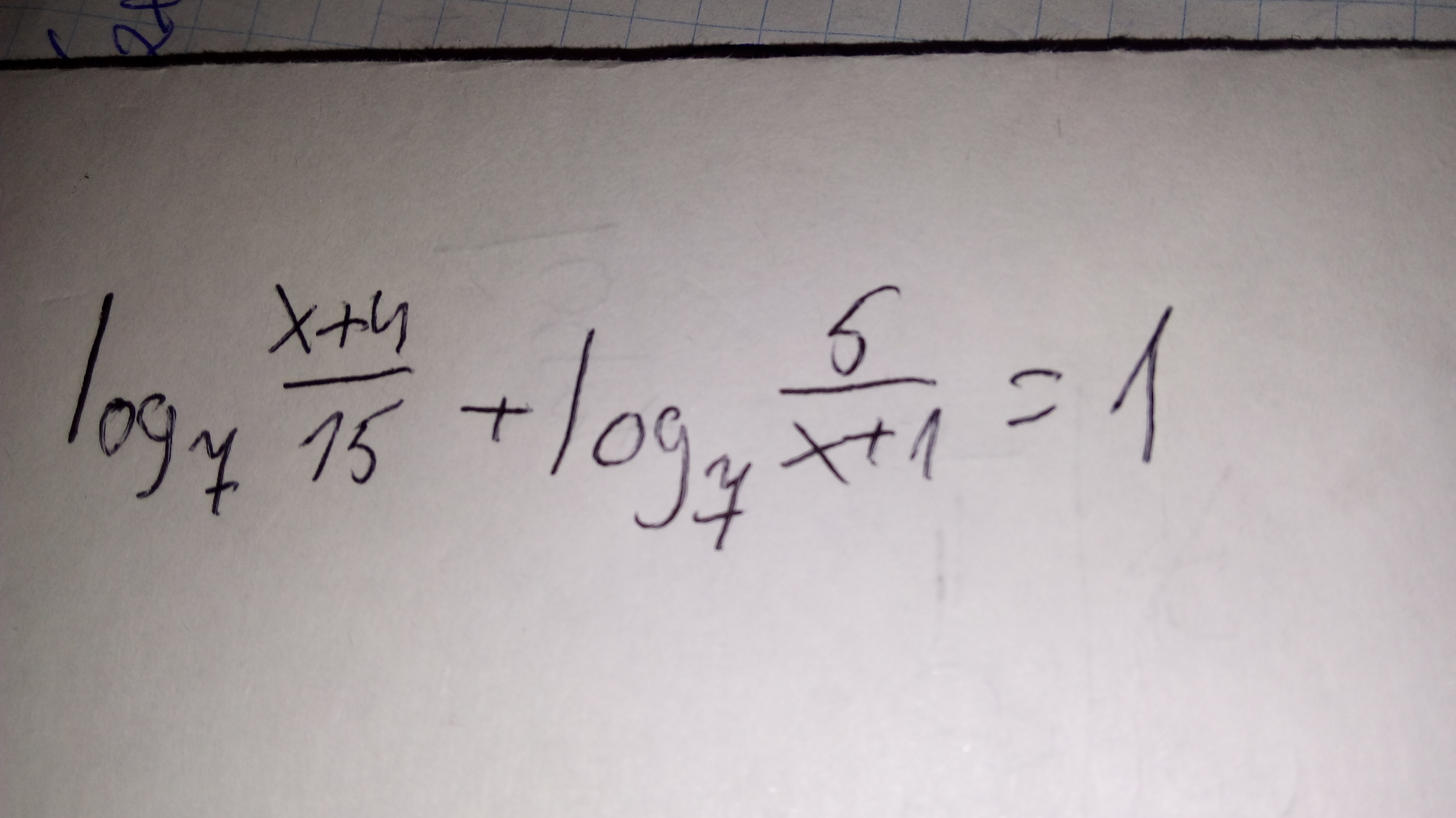
Ответы
Автор ответа:
1
х+1≠0
х≠ -1

x∈(-1; +∞)

x = -0.85
х≠ -1
x∈(-1; +∞)
x = -0.85
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: bajtusovamadina
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Биология,
автор: titov5645
Предмет: Математика,
автор: никаа4
Предмет: Математика,
автор: даринакузьмина