Question

Скласти рівняння дотичної до графіка ф-ції y=x^3 у точці (2;8) 

Answer 1

ДАНО
F = x³
Xo = 2
НАЙТИ
Уравнение касательной.
РЕШЕНИЕ
Уравнение касательной по формуле
Y = F'(x)*(x - Xo) +F(Xo).
Находим производную.
F'(x) = 3*x².
Находим значение в точке Xo = 2.
F'(2) = 3*2² = 3*4 = 12
F(2) = 2³ = 8 (дано - координата точки)
Подставили и получили
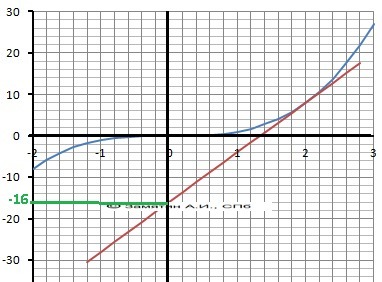
Y = 12*(x - 2) + 8 = 12*x - 16
ОТВЕТ:  12*х - 16 - уравнение касательной. 
Рисунок с графиками - в приложении.