Question

Помогите решить, пожалуйста. 15б.

Answer 1

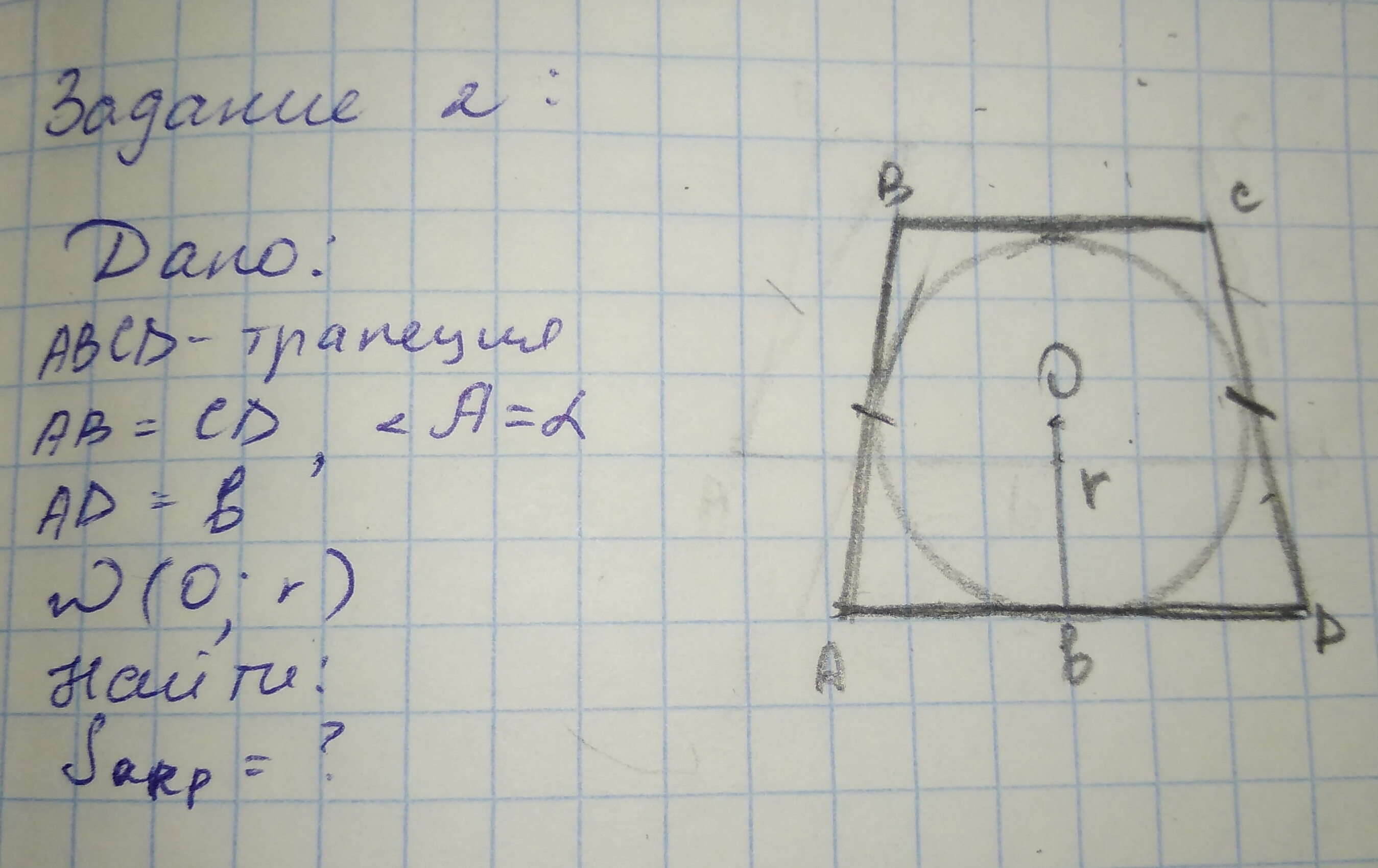
Т.к. окружность вписанная, то ее центр лежит на пересечении биссектрис углов трапеции. Таким образом AO - биссектриса. И DO - биссектриса. Опустим перпендикуляр OH к прямой AD из т. O. 
У равнобочной трапеции углы при основании равны, поэтому <A = <D. И
<A/2 = <OAH = <OBH = <B/2.
Треугольники OAH и OBH прямоугольные с равным острым углом, значит и третьи углы у них равны, поскольку они дополняют сумму двух первых до 180 градусов, то есть <AOH=<BOH.
Треугольники AOH и BOH равны по стороне (OH) и прилежащим к ней углам. Поэтому из равенства треугольников следует, что AH = DH = b/2.
Из прямоугольного треугольника AOH получаем
tg(<OAH) = r/AH, то есть tg(α/2) = r/(b/2) = 2r/b,
выразим отсюда r
r = b*tg(α/2)/2.
Площадь окружности = π*r^2 = π*(b*tg(α/2)/2)² = (π/4)*(b*tg(α/2))².