Question

Промежутки монотонности функции и точки экстремумы y=x^5-x^3+x+2

Answer 1

ДАНО
y = x⁵ - x³ + x +2
РЕШЕНИЕ
1. Область определения - Х∈(-∞;+∞) - непрерывная.
2. Первая производная - поиск экстремумов.
Y'(x) = 5*x⁴ - 3*x² +1= 0.
Корней нет - нет экстремумов. Возрастает во всем интервале существования.
3. Вторая производная - поиск точек перегиба.
Y"(x) = 20*x³ - 6*x = 2*x*(10*x² - 3) = 0
Корни - точки перегиба:  x₁ = 0, x₂ = -√30/10 ≈ - 0.55, x₃ = √30/10 ≈ 0.55
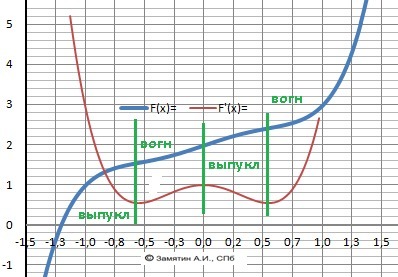
Выпуклая: X∈(-∞;x2)∪(0;x3)
Вогнутая: X∈(x2;0)∪(x3;+∞)
Рисунок с графиком в приложении.