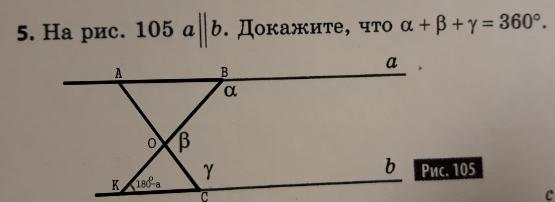На рисунке 105 a параллельна b. Докажите, что

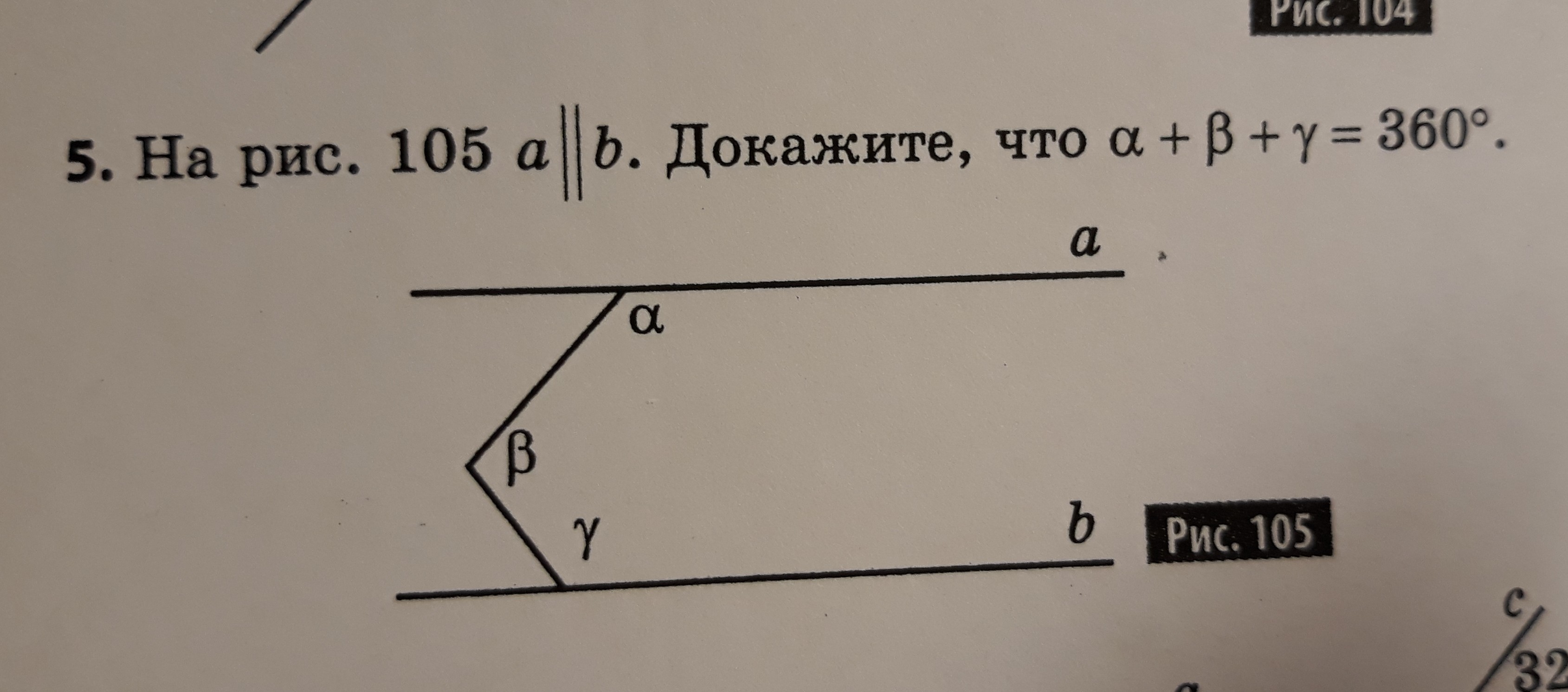
Ответы
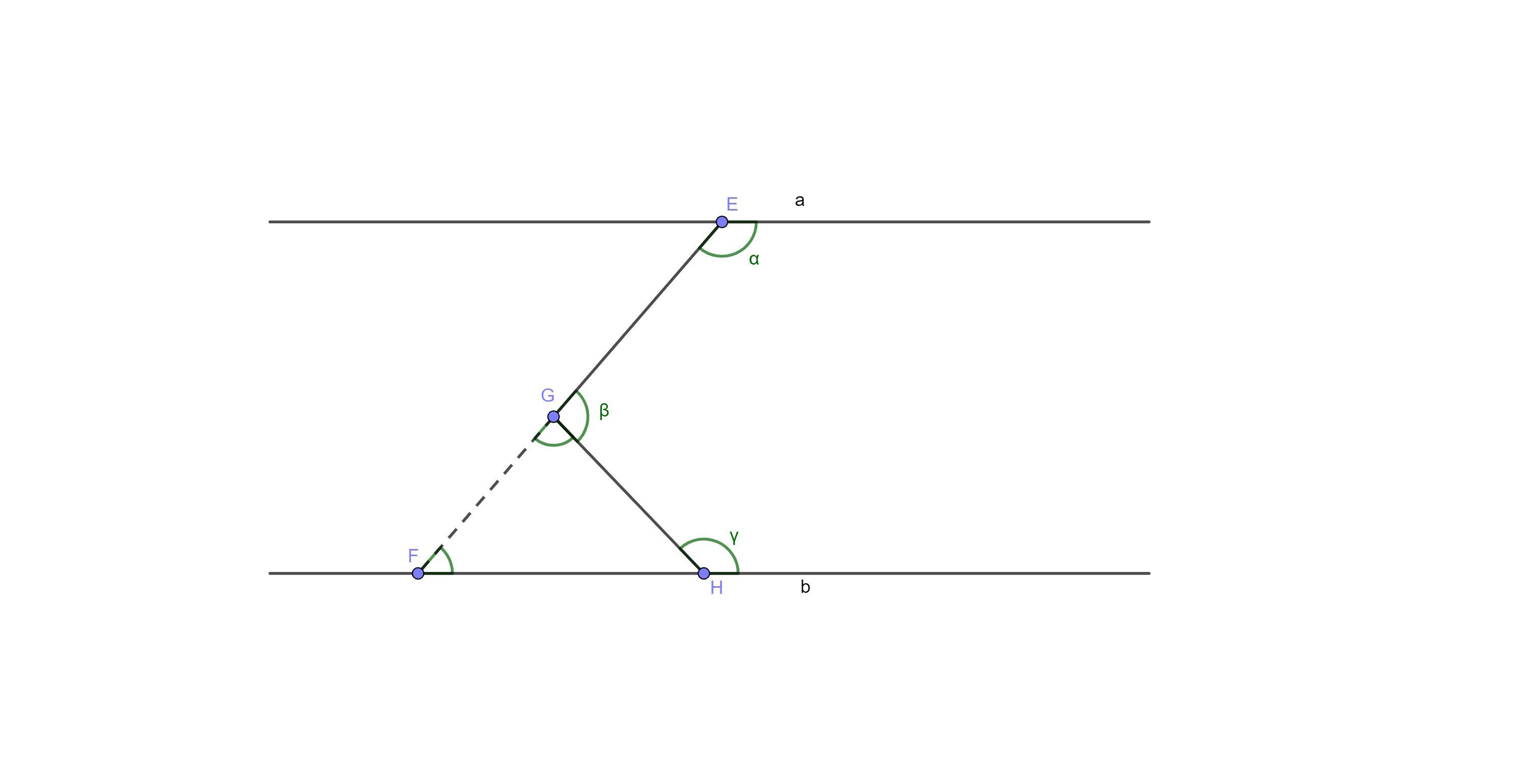
Рисунок во вложении
Дано:
a║b
Доказать: α + β + γ = 360°
Продолжим отрезок EG до пересечения с прямой b. Отрезок EG будет пересекать прямую b в точке F.
Рассмотрим треугольник FGH
γ = ∠F + ∠FGH (Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним)
∠FGH = 180° - β т.к. ∠FGH и β являются смежными
∠F = 180° - α как односторонние углы при a║b и секущей FE
Что и требовалось доказать.
Дано :
a ║ b.
Доказать :
∠α + ∠β + ∠γ = 360°.
Доказательство :
Продлим прямые и обозначим вершины как показано на рисунке во вложении.
- При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180°.
Отсюда -
∠α + ∠ВКС = 180°
∠ВКС = 180° - ∠α.
- Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Следовательно -
∠ОКС + ∠ОСК = ∠β
180° - ∠α + ∠ОСК = ∠β
Но -
∠γ + ∠ОСК = 180° (так как смежные)
∠ОСК = 180° - ∠γ.
Можем подставить в формулу -
180° - ∠α + ∠ОСК = ∠β
180° - ∠α + 180° - ∠γ = ∠β
360° - ∠α - ∠γ = ∠β.
Подставим это значении в формулу, которую нам нужно доказать, и посмотрим, что выйдет -
∠α + ∠β + ∠γ = 360°
∠α + 360° - ∠α - ∠γ + ∠γ = 360°
360° = 360°.
Получили верное равенство. Следовательно, формула, которую нужно доказать, верна.
Ответ :
Что требовалось доказать.