Question

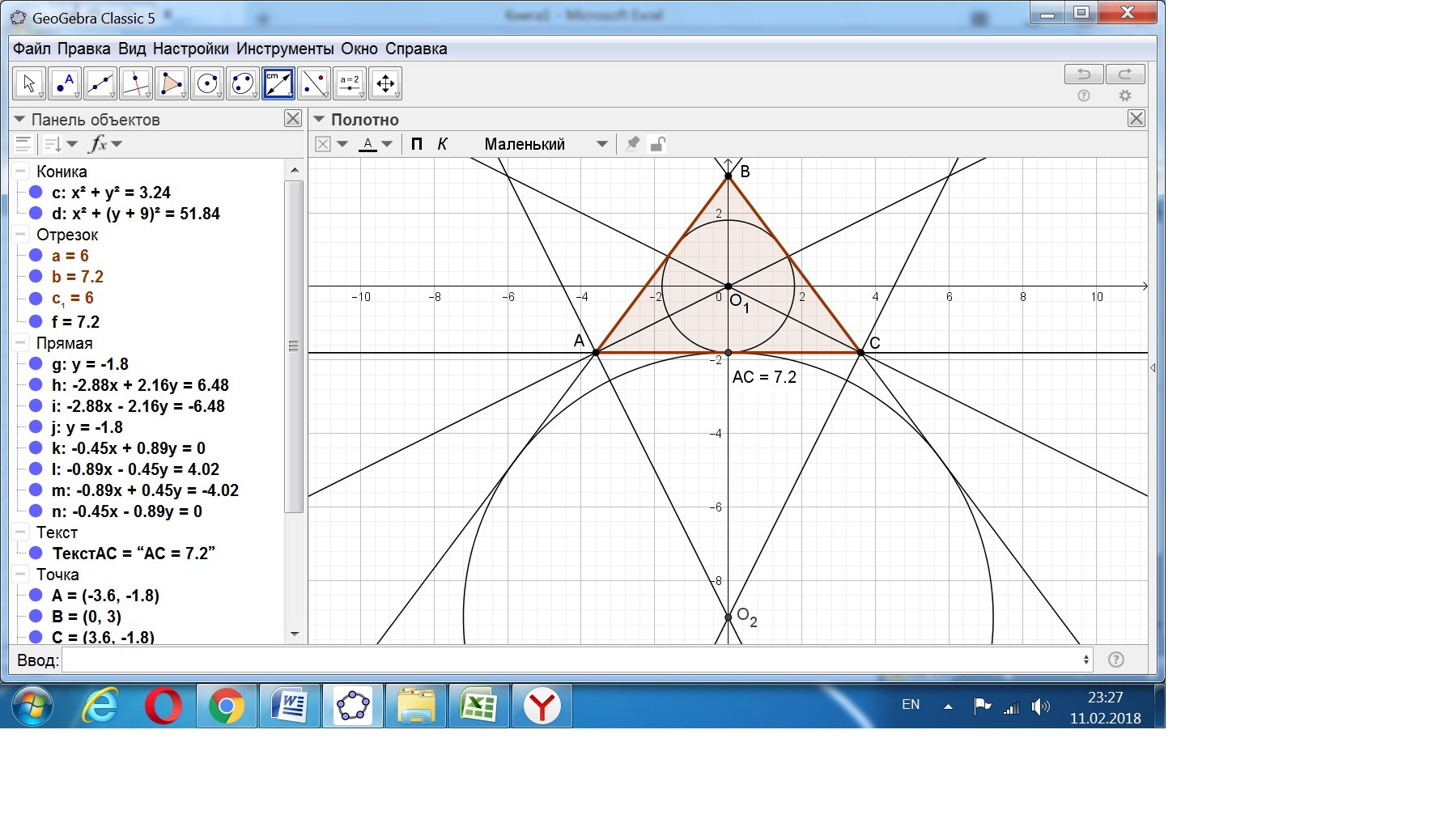
ABC - равнобедренный треугольник с основанием AC. Окружность радиуса 7,2 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Радиус окружности, вписанной в треугольник ABC равен 1,8. Найдите основание треугольника AC.

Answer 1

Обозначим радиус 1,8 - r, а 7,2 - R
Тангенс половины угла С равен:
tg(C/2) = r/(AC/2) = 2r/AC = 3,6/АС.
Половина внешнего угла С равна (180-С)/2 = 90 - (С/2).
Тангенс такого угла по формуле приведения равен котангенсу (С/2).
tg(90 - (С/2)) = 7,2/(AC/2) = 14,4/AC.
ctg(C/2) = AC/2r = АС/3,6.
Приравниваем: АС/3,6 = 14,4/АС,
Отсюда АС = √(3,6*14,4) = √ 51,84 = 7,2.