Предмет: Информатика,
автор: Аноним
Требуется найти все корни уравнения с точностью не ниже 10⁻¹².
Уравнение имеет вид

Вот решение на PascalABCNET 3.3, сборка 1627 от 27.01.2018:
uses NumLibABC;
begin
var f:real->real:=x->Sqrt(Abs(x+3))-Cos(0.387*x);
var oL:=new RootsIsolation(f,-10,10,0.1);
var oZ:=new Zeroin(f,1e-12);
foreach var r in oL.Value do
oZ.Value(r[0],r[1]).Println
end.
Найдены корни
-3.1250285461067
-2.77171087522778
Интересует решение другим путем (назовем его "школьным" или "студенческим") на любом из языков Pascal, C/C++/C#, Basic.
Exponena:
Студентом бы я мог использовать метод "вилки" достаточно прост для реализации (когда-то и делал). Правда сначала требуется "изолировать" все корни. Для любого уравнения автоматический гарантированный поиск всех корней не представляю. Н вот конкретно это. Достаточно рассмотреть только отрезок, являющийся решением неравенства |x+3|<=1.
Ответы
Автор ответа:
19
Ну раз никто не решился, а может не захотел возиться, покажу я вам динозавра!
У меня когда-то была программа на QBASIC. (Первая личный комп вначале был без жёсткого диска. Под DOS грузили с дискеты. И там этот мелкий интерпретатор (ок 190 кБайт) был неплохим подспорьем.)
Программа сохранилась. Она изначально только график рисовала. Потом я её дополнял. В том числе и решением уравнений вилкой. Было несколько версий Функцию я по-быстрому заменил на требуемую в задаче. Перелопачивать и выяснять полностью состояние программы не стал.
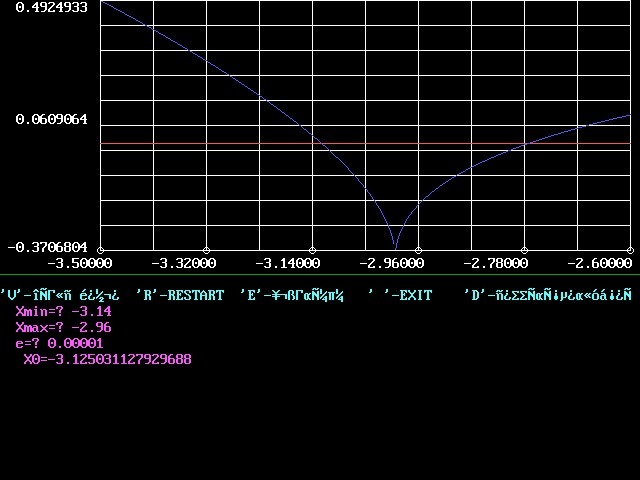
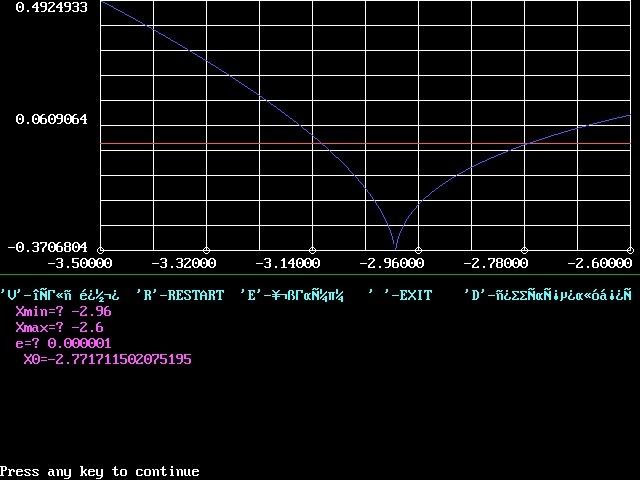
За требуемую точность не поручусь. Но 4-6 знаков после запятой выдам. Это был "Полуавтоматический" вариант с прорисовкой графика. Красной линией прочерчивалась прямая y=0. График можно было перерисовывать, задавая новые пределы изменения переменной х. Глядя на график можно было определить исходные отрезки для запуска метода вилки.
На скринах, естественно, проблемы с кириллицей. (Ненастроенный DosBox) Но текст программы загнал в pdf. Там можно прочесть все надписи.
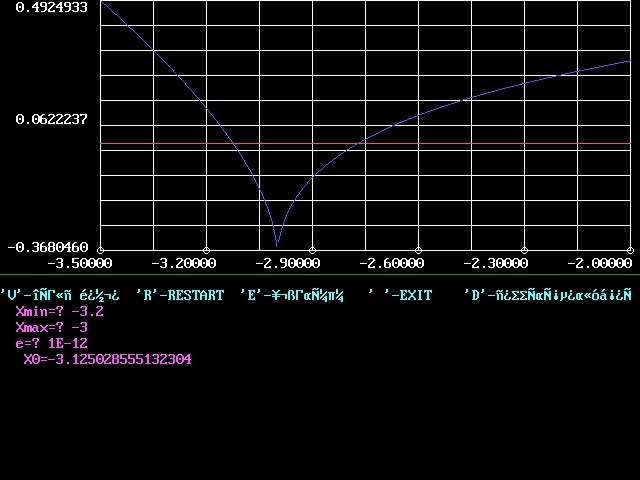
На 3-м снимке видно, что, потребовав точность , я получил ответ, отличающийся от ответа МАСТЕРА. Я так думаю, что у меня не все переменные, требуемые для расчёта объявлены с двойной точностью. (Изначально таких там вообще не было). Но 7 знаков после запятой в ответе совпадают. :) А может это ограничение демоверсии QBASIC интерпретатора.
, я получил ответ, отличающийся от ответа МАСТЕРА. Я так думаю, что у меня не все переменные, требуемые для расчёта объявлены с двойной точностью. (Изначально таких там вообще не было). Но 7 знаков после запятой в ответе совпадают. :) А может это ограничение демоверсии QBASIC интерпретатора.

У меня когда-то была программа на QBASIC. (Первая личный комп вначале был без жёсткого диска. Под DOS грузили с дискеты. И там этот мелкий интерпретатор (ок 190 кБайт) был неплохим подспорьем.)
Программа сохранилась. Она изначально только график рисовала. Потом я её дополнял. В том числе и решением уравнений вилкой. Было несколько версий Функцию я по-быстрому заменил на требуемую в задаче. Перелопачивать и выяснять полностью состояние программы не стал.
За требуемую точность не поручусь. Но 4-6 знаков после запятой выдам. Это был "Полуавтоматический" вариант с прорисовкой графика. Красной линией прочерчивалась прямая y=0. График можно было перерисовывать, задавая новые пределы изменения переменной х. Глядя на график можно было определить исходные отрезки для запуска метода вилки.
На скринах, естественно, проблемы с кириллицей. (Ненастроенный DosBox) Но текст программы загнал в pdf. Там можно прочесть все надписи.
На 3-м снимке видно, что, потребовав точность
Приложения:
Это понятно. Ладно, я хоть теперь знаю название алгоритма. При необходимости можно посмотреть хотя бы.
Руководство поABC? Давайте
Пусть так. Саму реализацию метода вы хотели предложить?
Похожие вопросы
Предмет: Геометрия,
автор: 12jana34
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: dfdgfgfggfedf
Предмет: Математика,
автор: richerik
Предмет: Литература,
автор: Marisha5551