Предмет: Геометрия,
автор: Sadkosi
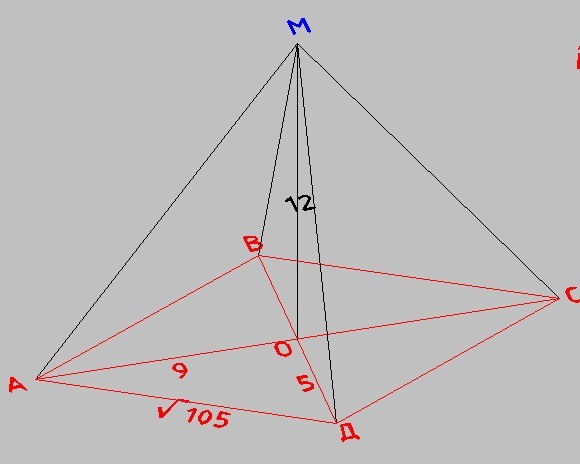
1. Через точку пересечения диагоналей ромба АВСD проведен к его плоскости
перпендикуляр МО длиной 12 см. Диагонали ромба равны 18 см и 10 см. Вычислите:
- длины наклонных МА, МВ, МС, MD
- расстояние между основаниями этих наклонных
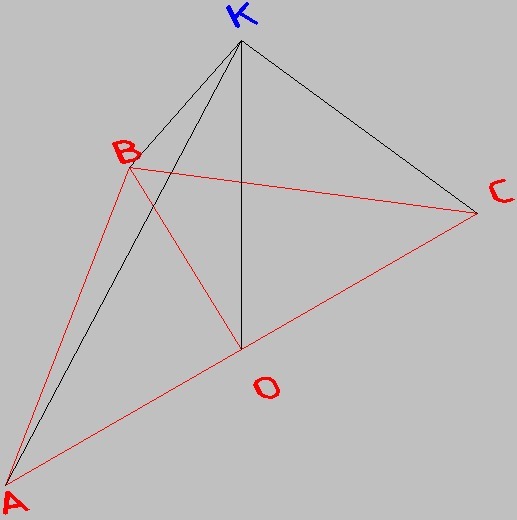
2. Через середину гипотенузы прямоугольного треугольника АВС проведен к его плоскости
перпендикуляр КО, равный 8,5 см. ВС = 8 см, АС = 15 см. Вычислите углы между
плоскостью треугольника и наклонными КА, КВ, КС.
Ответы
Автор ответа:
9
АО = СО = 9 см
ВО = ДО = 5 см
АМ = СМ = √(9²+12²) =√(81+144) = √225 = 15 см
МС = МД = √(5²+12²) =√(25+144) = √169 = 13 см
Расстояния между основаниями? Это как? Стороны и диагонали ромба?
AB = BC = СД = АД = √(9²+5²) =√(81+25) = √106 см
АС и ВД даны по условию.
---
2 варианта, к сожалению!
1) АС - гипотенуза
AO = AC/2 = 7,5 см
О - центр описанной окружности треугольника АВС и поэтому
АК = ВК = СК = √(7,5² + 8,5²) = √(15² + 17²)/2 = √(225+289)/2 = √514/2 см
2) AB - гипотенуза
АВ = √(8² + 15²) = √(64+225) = √289 = 17 см
AO = AВ/2 = 8,5 см
АК = ВК = СК = √(8,5² + 8,5²) = 8,5√2 см
ВО = ДО = 5 см
АМ = СМ = √(9²+12²) =√(81+144) = √225 = 15 см
МС = МД = √(5²+12²) =√(25+144) = √169 = 13 см
Расстояния между основаниями? Это как? Стороны и диагонали ромба?
AB = BC = СД = АД = √(9²+5²) =√(81+25) = √106 см
АС и ВД даны по условию.
---
2 варианта, к сожалению!
1) АС - гипотенуза
AO = AC/2 = 7,5 см
О - центр описанной окружности треугольника АВС и поэтому
АК = ВК = СК = √(7,5² + 8,5²) = √(15² + 17²)/2 = √(225+289)/2 = √514/2 см
2) AB - гипотенуза
АВ = √(8² + 15²) = √(64+225) = √289 = 17 см
AO = AВ/2 = 8,5 см
АК = ВК = СК = √(8,5² + 8,5²) = 8,5√2 см
Приложения:
Sadkosi:
Благодарю.
Похожие вопросы
Предмет: Геометрия,
автор: neeehto
Предмет: Математика,
автор: keshakaef29
Предмет: Другие предметы,
автор: nikolovasofia123
Предмет: Математика,
автор: dairov20040814
Предмет: Математика,
автор: rabilos56