Question

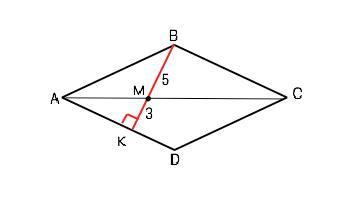
В ромбе АВСД бОльшая диагональ АС делит высоту ВК на ВМ=5см и МК=3см. Найти площадь ромба.

Answer 1

Ответ: 80 см²

Объяснение: Диагонали ромба - биссектрисы его углов. В прямоугольном треугольнике АВК отношение гипотенузы АВ к катету ВК равно отношению отрезков. на которые биссектриса  угла А делит высоту ВК: АВ:АК=5:3 - это отношение гипотенузы и катета «египетского» треугольника.  Тогда ВК:АВ=4:5, Т.к. ВК=3+5=8,  АВ=AD=10 см. Ѕ=ВК•AD=8˙10=80 см²

Или:

В ∆ АВК биссектриса АМ делит сторону ВК в отношении сторон, между которыми она проведена. Т.е. АВ:АК=ВМ:МК. Примем коэффициент отношения сторон равным а. Тогда АК=3а, АВ=5а.

  По т.Пифагора  АВ²-АК²=ВК².    

ВК=ВМ+МК=5+3=8⇒

25а²-9а²=64

16а²=64,  а*=4, а=√4=2

Сторона ромба =2•5=10

Площадь ромба равна произведению высоты на сторону.

Ѕ=АD•АК=10•8=80 см²