Предмет: Геометрия,
автор: Аноним
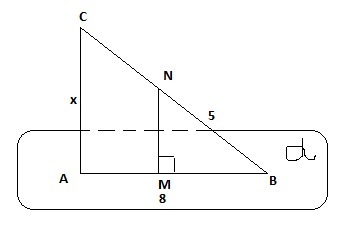
Точки А и В лежат, а точка С не лежит в плоскости альфа. Точки М и N -середины отрезков АВ и ВС, МN перпендикулярны альфа, АВ=8, ВN=5. Найдите расстояние от точки С до плоскости альфа.
Ответы
Автор ответа:
13
MN - средняя линия треугольника ABC. Поскольку по условию MN⊥ плоскости α, а AC║MN⇒AC⊥α⇒AC равно расстоянию от C до α, которое и требуется найти. Поскольку CAB прямоугольный Δ (∠CAB=90°, так как прямая, перпендикулярная плоскости, перпендикулярна любой прямой, лежащей в этой плоскости), для нахождения AC можно применить теорему Пифагора
AC²=BC²-AB²=100-64=36=6²; AC=6.
Ответ: 6
AC²=BC²-AB²=100-64=36=6²; AC=6.
Ответ: 6
Автор ответа:
8
По условию CN=NB, AM=MB, значит MN- средняя линия ΔАВС.
Тогда АС=2MN
MN=√(NB²-MB²)=√(25-16)=3
АC=2MN=2*3=6
Тогда АС=2MN
MN=√(NB²-MB²)=√(25-16)=3
АC=2MN=2*3=6
Приложения:
Похожие вопросы
Предмет: Биология,
автор: dianabolybash
Предмет: История,
автор: vldmslvskj
Предмет: История,
автор: areniypolchuk
Предмет: Литература,
автор: ffg414507
Предмет: Математика,
автор: NFSJ