Question

1) Периметр правильного шестиугольника вписанного в окружность,равен 48м. Найди сторону квадрата,вписанного в ту же окружность.
2)Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72√3 см2
3)Найдите площадь кругового сектора, если градусная мера его дуги равна 120 градусам, а радиус круга равен 12см.

Answer 1

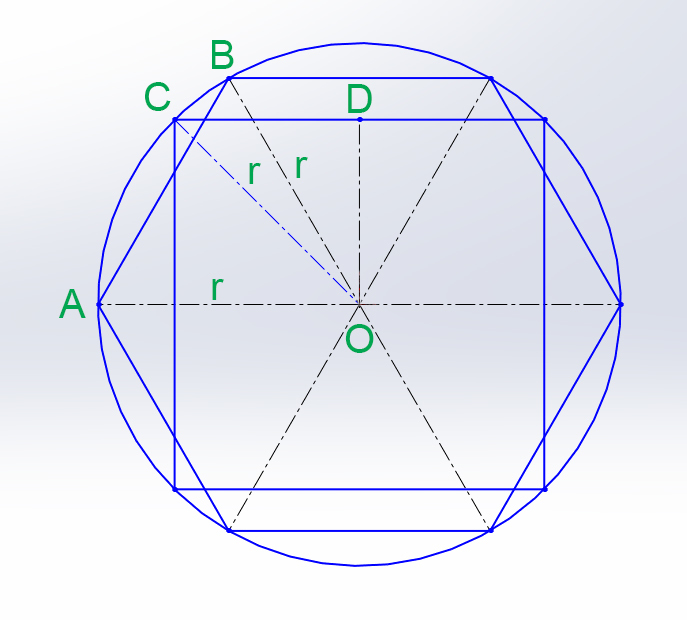
См. рисунок

1. Правильный шестиугольник, состоит из шести равносторонних треугольников.

Найдем сторону шестиугольника AB=r=48/6=8м.

Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD

По теореме Пифагора найдем  СD

r²=CD²+DO²=2CD² ⇒ r=CD√2⇒$CD=\frac{r}{\sqrt{2} }= \frac{8}{\sqrt{2}}$ м

$a=2*\frac{8}{\sqrt{2}}=8\sqrt{2}$ м

2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.

Площадь правильного шестиугольника равна

$S=\frac{3\sqrt{3}r^{2}}{2}$ ⇒

$r=\sqrt{\frac{2S}{3\sqrt{3}}}=\sqrt{\frac{2*72\sqrt{3}}{3\sqrt{3}}}=\sqrt{48}=4 \sqrt{3}$ см

Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см

3.  Площадь сектора равна

$S=\pi r^{2} *\frac{n}{360}= \pi 12^{2} \frac{120}{360} =\pi \frac{144}{3}$≈151 см²

(где n - градусная мера дуги сектора)