Предмет: Математика,
автор: Ammer
Найти производную 11^11*√2x^4-1/x
Приложения:
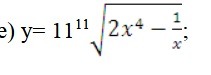
makuzkinap195y6:
Так 11 в 11 степени или 11 умножить на корень 11-й степени из выражения?
Почему удалили моё задание, вы спервы узнайте потом удаляйте, выше фото он написал 11 в степени 11 умножить на квадратный корень , вы удалили моё решение просто так, я требую объяснение!
121=11·11, т.е. 11^2. Неправильно была взята производная от предполагаемого квадратного корня. Т.е. решение было неправильным в любом случае
Ты косой или что, задание было квадратный корень производная 1/2 корень из х и ещё производная внутри корня
как таких модераторов берут ,если ты стажёр иди учи правила
Производная от корня=1/(2корня) · производную от подкоренного выражения.
я тоже самое написал
С точки зрения математики у Вас написано: 1/2·корень, т.е. (1/2)·(корень) или (корень)·(1/2) из-за того, что Вы не поставили в нужных местах скобки, а умножение и деление имеют равный приоритет.
Мы же не знаем, что Вы имели в виду, а проверяем по факту.
Ответы
Автор ответа:
0
Перепишем выражение для функции в виде y(x)=11*(2*x⁴-x⁻¹)^(1/11). Тогда y'(x)=11*1/11*[(2*x⁴-x⁻¹)^(-10/11)]*(2*4*x³-(-1)*x⁻²)=[(2*x⁴-1/x)^(-10/11)]*(8*x³+1/x²). Ответ: y'(x)=[(2*x⁴-1/x)^(-10/11)]*(8*x³+1/x²).
Похожие вопросы
Предмет: Алгебра,
автор: dagrid08
Предмет: Русский язык,
автор: kovelerdiana17
Предмет: История,
автор: dasanikolaevna992
Предмет: Обществознание,
автор: ketrien