Предмет: Математика,
автор: Курбан111о
помогите решить неравенство хотябы одно
Приложения:
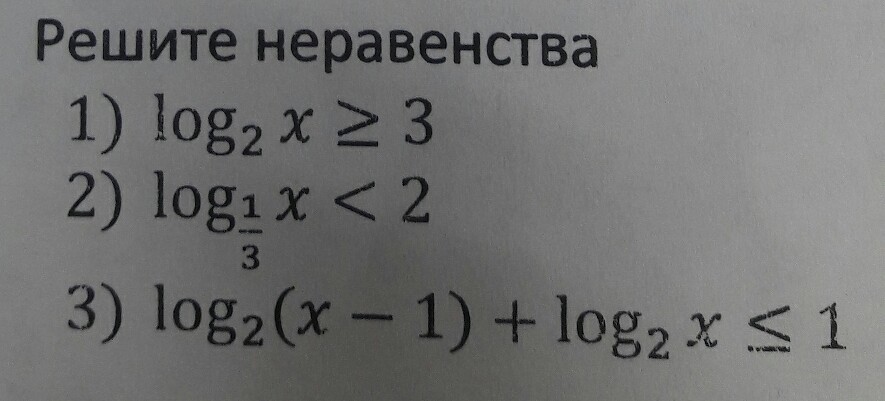
Ответы
Автор ответа:
0
log₂x≥3
x≥2³
x≥8.
log₁/₃ (x)<2
x>(1/3)²
x>1/9.
log₂(x-1)+log₂x≤1 ОДЗ: x-1>0 x>1 x>0 ⇒x∈(1;+∞)
log₂((x-1)*x)≤log₂2
(x-1)*x≤2
x²-x-2≤0
x²-x-2=0 D=9
x₁=2 x₂=-1
(x-2)*(x+1)≤0
-∞_____+____-1____-____2____+____+∞ ⇒
x∈[-1;2].
Cогласно ОДЗ: х∈(1;2].
x≥2³
x≥8.
log₁/₃ (x)<2
x>(1/3)²
x>1/9.
log₂(x-1)+log₂x≤1 ОДЗ: x-1>0 x>1 x>0 ⇒x∈(1;+∞)
log₂((x-1)*x)≤log₂2
(x-1)*x≤2
x²-x-2≤0
x²-x-2=0 D=9
x₁=2 x₂=-1
(x-2)*(x+1)≤0
-∞_____+____-1____-____2____+____+∞ ⇒
x∈[-1;2].
Cогласно ОДЗ: х∈(1;2].
Автор ответа:
0
1) основание логарифма больше 1, знак неравенства сохраняется
x ≥ 2³
x ≥ 8
2) основание логарифма меньше 1, знак неравенства
x > (1/3)²
x > 1/9
3) log2(x-1)+log2(x) ≤ 1
О.Д.З:
{x-1 > 0 {x > 1
{x > 0 {x >0
x > 1
log2(x²-x) ≤ 1
x²-x ≤ 2
x²-x-2 ≤ 0
(x+1)(x-2) ≤ 0
x ∈ [-1; 2]
С О.Д.З.: x ∈ (1; 2]
x ≥ 2³
x ≥ 8
2) основание логарифма меньше 1, знак неравенства
x > (1/3)²
x > 1/9
3) log2(x-1)+log2(x) ≤ 1
О.Д.З:
{x-1 > 0 {x > 1
{x > 0 {x >0
x > 1
log2(x²-x) ≤ 1
x²-x ≤ 2
x²-x-2 ≤ 0
(x+1)(x-2) ≤ 0
x ∈ [-1; 2]
С О.Д.З.: x ∈ (1; 2]
Похожие вопросы
Предмет: Алгебра,
автор: aleksandranedohodova
Предмет: Математика,
автор: miyash81
Предмет: Русский язык,
автор: savinasofa908
Предмет: Химия,
автор: devmad12