Предмет: Алгебра,
автор: yulechkakiryan
помогите пожалуйста решить неравенство
Приложения:
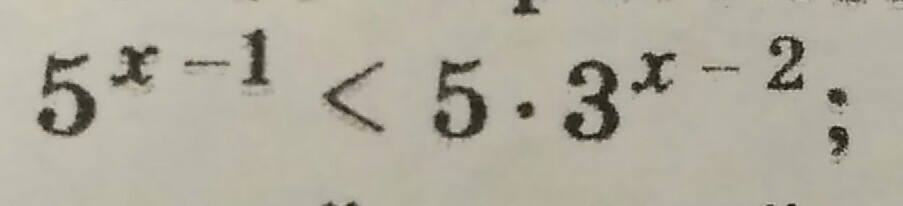
Ответы
Автор ответа:
1
Умножив на 5 обе части неравенства, получим:
Степень 3ˣ положительна при любом значении х, поэтому знак неравенства не изменится, если обе его части разделить на 3ˣ.
При равных основаниях, больших 1, знак неравенства для показателей степеней не изменится, поэтому:
Ответ: х ∈]-∞; 2[
Похожие вопросы
Предмет: Литература,
автор: imangaliaana
Предмет: Литература,
автор: hollxme
Предмет: Английский язык,
автор: nurzhaunurdaulett
Предмет: Геометрия,
автор: abdulova200658
Предмет: Литература,
автор: anastasiachupina61