Предмет: Геометрия,
автор: miha2855
Какую наибольшую площадь может иметь параллелограмм со сторонами 12 см 18 см?
Ответы
Автор ответа:
0
площадь будет наибольшей, если этот параллелограмм будет прямоугольником.
Sпараллелограмма = a*b*sin(x)
синус угла --число, всегда меньшее 1 (по модулю),
максимальное его значение sin(90°) = 1
при умножении на число, меньшее 1, площадь будет только уменьшаться... 12*18 = 216
Sпараллелограмма = a*b*sin(x)
синус угла --число, всегда меньшее 1 (по модулю),
максимальное его значение sin(90°) = 1
при умножении на число, меньшее 1, площадь будет только уменьшаться... 12*18 = 216
Автор ответа:
0
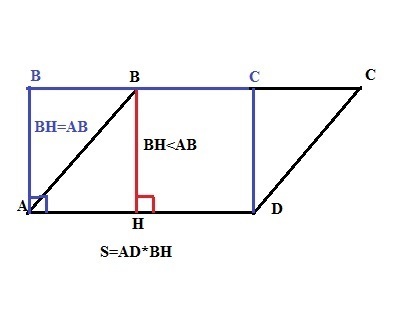
Площадь параллелограмма АВСD равна произведению его стороны AD на высоту BH, опущенную на эту сторону. Так как перпендикуляр из точки на прямую всегда меньше наклонной, проведенной из этой точки к данной прямой, то произведение AD*ВН , будет максимальным, когда ВН=ВА, то есть когда параллелограмм является прямоугольником.
Приложения:
Похожие вопросы
Предмет: История,
автор: aorlovbobruisk
Предмет: Литература,
автор: anna52045
Предмет: Литература,
автор: laptutanasta
Предмет: Алгебра,
автор: Иришенскаянская
Предмет: История,
автор: dan913