Question

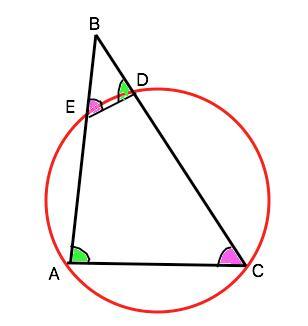
Через вершины А и С неравнобедренного треугольника АВС проведена окружность, которая пересекает стороны ВА и ВС в точках Е и Д соответственно. Какое из данных равенств является верным?
ВС/ВД=ВА/ВС
ВЕ/ВС=ВД/ВА
ДЕ/АС=ВД/ВС
ВД/ДЕ=ВС/АС

Answer 1

Ответ: ВЕ/ВС=ВD/ВА

Объяснение: Четырехугольник АЕDC - вписанный. Сумма противоположных углов вписанного четырехугольника 180°.

 Угол ЕDС+угол ЕАС=180°. Поэтому ∠ ВDЕ=∠ВАС. Аналогично ∠ВЕD=∠ВСА.  Угол В треугольников АВС и ВЕD общий ⇒ Треугольники АВС и ВЕD подобны по равенству углов. В подобных треугольниках сходственные стороны ( лежащие против равных углов)  пропорциональны. ⇒

ВЕ/ВС=ВD/ВА