Question

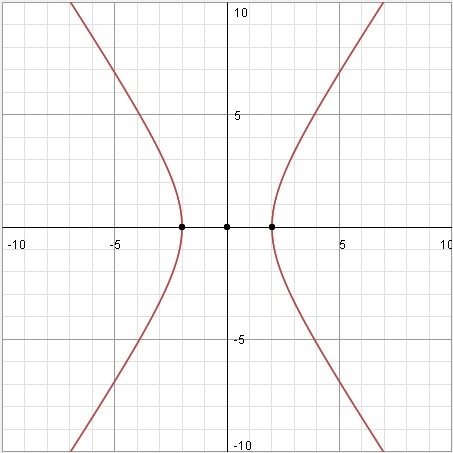
Найдите длины полуосей,координаты фокусов, эксцентриситет ∈ гиперболы $9 x^{2} -4y^{2} -36=0$. Изобразите гиперболу на чертеже. Пожалуйста помогите.

Answer 1

$frac{x^2}{4} - frac{y^2}{9} =1$
$frac{(x-h)^2}{a^2} - frac{(y-k)^2}{b^2} =1$
$a=2$
$b=3$
$k=0$
$h=0$
$(0;0)$
$sqrt{13}$
$(2;0);(-2;0)$
$( sqrt{13} ;0);(- sqrt{13};0)$
$frac{ sqrt{13} }{2}$
$frac{9 sqrt{13} }{ sqrt{13} }$
$y=$±$frac{3}{2} x+0$
$y= frac{3x}{2}$
$y=- frac{3x}{2}$
$y= frac{3x}{2} ;y=- frac{3x}{2}$
Эти величины представляют важные значения для построения графика и анализа гиперболы.
Центр: $(0;0)$
Вершины: $(2;0);(-2;0)$
Фокусы: $( sqrt{13} ;0);(- sqrt{13} ;0)$
Эксцентриситет: $frac{ sqrt{13} }{2}$
Расстояние от фокуса до директрисы: $frac{9 sqrt{13} }{13}$
Асимптоты: $y= frac{3x}{2} ;y=- frac{3x}{2}$