Question

80 БАЛЛОВ ЗАДАЧА 7 КЛАССА
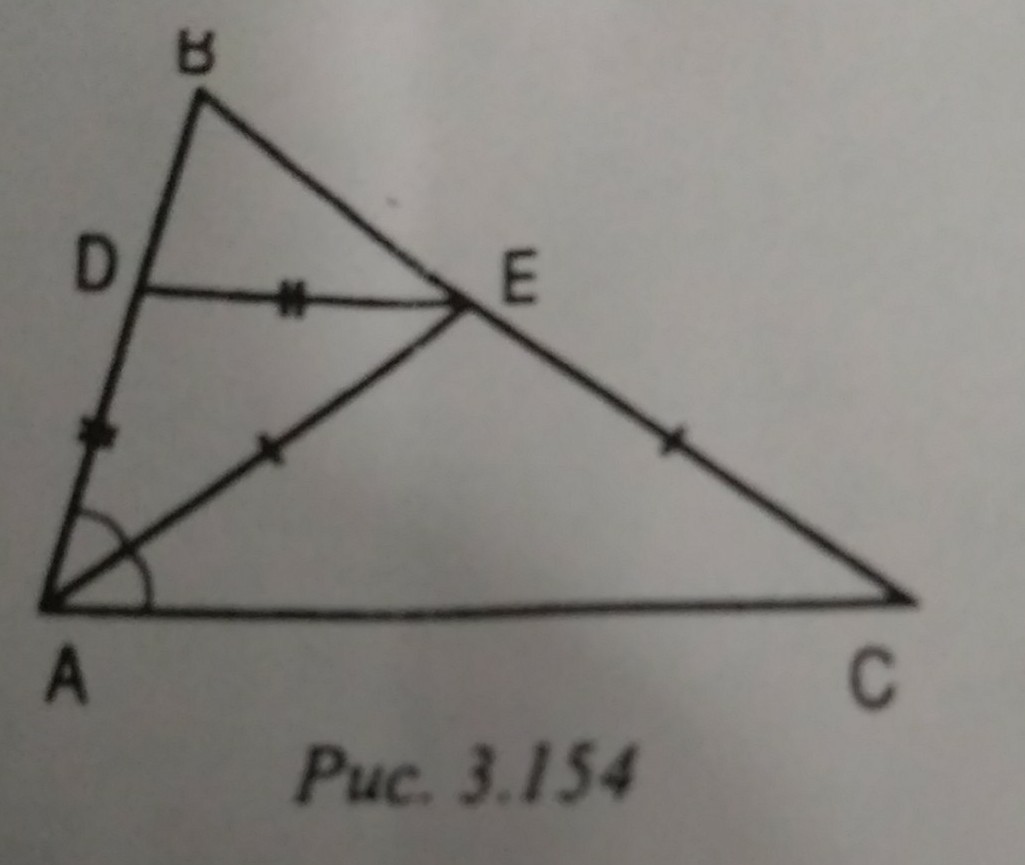
Дано: АЕ-биссектриса треугольника ABC, AD=DE АЕ=ЕС, угол АСВ-37градусов. Найти: угол BDE

Answer 1

Решение:
По условие AE = EC следовательно ▵AEC равнобедренный, а значит ∠EAC = ∠ECA = 37.
Так как AE биссектриса, следовательно ∠BAE = ∠EAC = ∠ECA = 37.
Рассмотрим ▵ADE, по условию AD = DE, следовательно ▵ADE - равнобедренный, а значит ∠DAE = ∠DEA = 37. Используя теорему о сумме углов (все углы треугольника равны 180), найдём ∠ADE.
∠ADE = 180 - 37 - 37 = 106. Заметим что ∠ADE и ∠EDB - смежные, тогда ∠BDE = 180 - ∠ADE = 180 - 106 = 74.
Ответ: 74

Answer 2

Ответ: 74°.
Решение прилагаю.