Предмет: Алгебра,
автор: nazarm378
Помогите, пожалуйста, найти наибольшее целое отрицательное решение неравенства с помощью методом интервалов
Приложения:
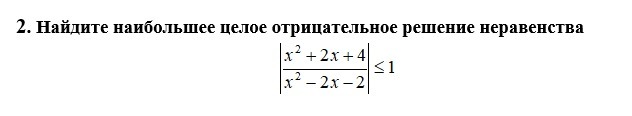
Ответы
Автор ответа:
0
составляем систему:

решаем каждое неравенство по отдельности:

используем метод интервалов(см. приложение 1)
![x in (-infty;- 1,5]cup (1-sqrt{3};1+sqrt{3}) x in (-infty;- 1,5]cup (1-sqrt{3};1+sqrt{3})](https://tex.z-dn.net/?f=x+in+%28-infty%3B-+1%2C5%5Dcup+%281-sqrt%7B3%7D%3B1%2Bsqrt%7B3%7D%29)
решаем 2 неравенство:

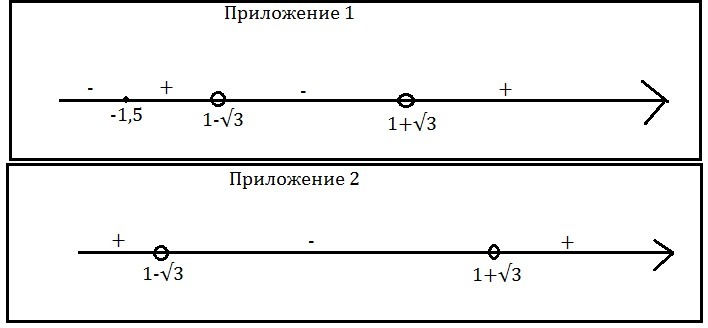
используем метод интервалов(см. приложение 2)

пересекаем множества решений этих двух неравенств:
![x in ((-infty;- 1,5]cup (1-sqrt{3};1+sqrt{3}))cap ((-infty;1-sqrt{3})cup (1+sqrt{3};+infty))\=(-infty;-1,5] x in ((-infty;- 1,5]cup (1-sqrt{3};1+sqrt{3}))cap ((-infty;1-sqrt{3})cup (1+sqrt{3};+infty))\=(-infty;-1,5]](https://tex.z-dn.net/?f=x+in+%28%28-infty%3B-+1%2C5%5Dcup+%281-sqrt%7B3%7D%3B1%2Bsqrt%7B3%7D%29%29cap++%28%28-infty%3B1-sqrt%7B3%7D%29cup+%281%2Bsqrt%7B3%7D%3B%2Binfty%29%29%5C%3D%28-infty%3B-1%2C5%5D)
наибольшее целое отрицательное: -2
Ответ: -2
решаем каждое неравенство по отдельности:
используем метод интервалов(см. приложение 1)
решаем 2 неравенство:
используем метод интервалов(см. приложение 2)
пересекаем множества решений этих двух неравенств:
наибольшее целое отрицательное: -2
Ответ: -2
Приложения:
Автор ответа:
0
Анонимус, скажи одну вещь, как здесь оказалось (-1,5) ?
Похожие вопросы
Предмет: Геометрия,
автор: evdokimov21
Предмет: Математика,
автор: kristinatsybukh1302
Предмет: Русский язык,
автор: chellsea08
Предмет: Алгебра,
автор: Masha708
Предмет: Литература,
автор: erkonya07