Предмет: Геометрия,
автор: RayRayRayRay
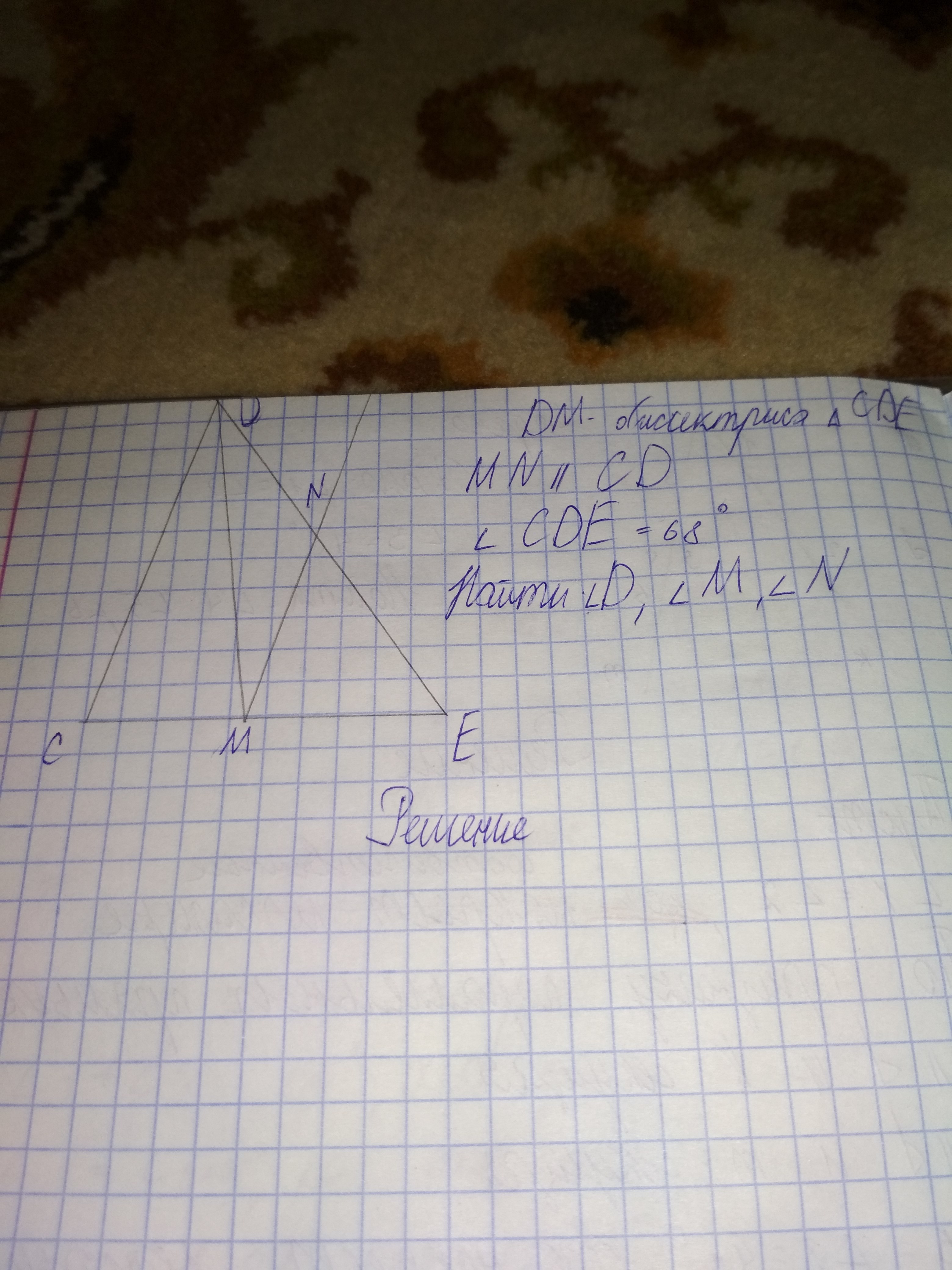
DM – биссектриса треугольника CDE. MN параллельно CD. Угол CDE = 68 градусов. Найти угол D, угол N, угол M.
Приложения:
Ответы
Автор ответа:
0
За условием DM - бисиктриса ΔCDE, тогда ∠СDM = ∠MDE = 68°. Если ΔСВМ - равнобедренный, то ∠DCE = ∠DMC. За теоремой про сумму углов треугольника ∠DCE + ∠DMC + ∠СDE = 180°. Тогда можем найти сумму ∠DCE и ∠DMC: 180° - ∠СDE = 180° - 68° = 112°. Теперь найдем ∠DCE и ∠DMC: 112° / 2 = 56°. Если MN║CD и СE - общая, то ∠DCE = ∠NME. Если ∠DCE = ∠DMC, то ∠NME = ∠DMC. За теоремой про смежные углы можем найти ∠DMN: 180° - (∠NME + ∠DMC) = 180° - (56° + 56°) = 68°. За теоремой про сумму углов треугольника ∠NME + ∠MDE + ∠DMN = 180°. Тогда можем найти ∠DNM: 180° - (∠DMN + ∠MDE) = 180° - (68° + 68°) = 44°
Ответ: 68°, 68°, 44°.
Ответ: 68°, 68°, 44°.
Автор ответа:
0
уверен, что есть другой более логичный способ решения этой задачи, но я сделал так.
Похожие вопросы
Предмет: Русский язык,
автор: demynchukmelana
Предмет: Математика,
автор: eluchechkaelochka
Предмет: Қазақ тiлi,
автор: zhan86715
Предмет: Математика,
автор: subbotin00
Предмет: Математика,
автор: 12355678910111213