Question

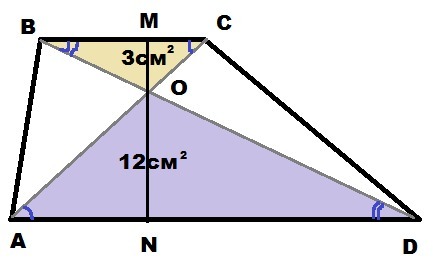
Помогите пожалуйста!Диагонали трапеции ABCD c основанием AD пересекаются в точке O,площади треугольников AOD и BOC равны 12 см² и 3 см².Найдите площадь трапеции.

Answer 1

В трапеции BC║AD  ⇒  
∠CBD = ∠BDA;  ∠BCA = ∠CAD - как  накрест лежащие   ⇒
ΔBOC подобен ΔAOD  по двум углам
Площади подобных треугольников относятся как коэффициент подобия в квадрате
$frac{S_{AOD}}{S_{BOC}} = frac{12}{3}=4= 2^2 = k^2$    ⇒
$frac{AD}{BC} = frac{ON}{OM} = k = 2$     ⇒
AD = 2BC;   ON = 2*OM
Высота трапеции равна сумме высот треугоьников
h = MN = OM + ON = OM + 2*OM = 3*OM

Площадь трапеции
$S = frac{AD + BC}{2} h = frac{2BC + BC}{2} *3*OM = \ \ = frac{3BC}{2} *3*OM = 9( frac{1}{2}BC*OM )= 9*S_{BOC}= 9*3 = 27$

Ответ: площадь трапеции  27 см²

Answer 2

Спасибо большое!