Предмет: Алгебра,
автор: annaKOTNK
Дам 80 баллов, помогите пожалуйста)
Приложения:
Ответы
Автор ответа:
0
1 задача
ax² + bx +c =0 - общий вид квадратного уравнения
х² + (b/a)x + c/a = 0 -приведённый вид квадратного уравнения, для которого выполняется теорема Виета:
x₁+x₂= - b/а
x₁ · x₂= c/а
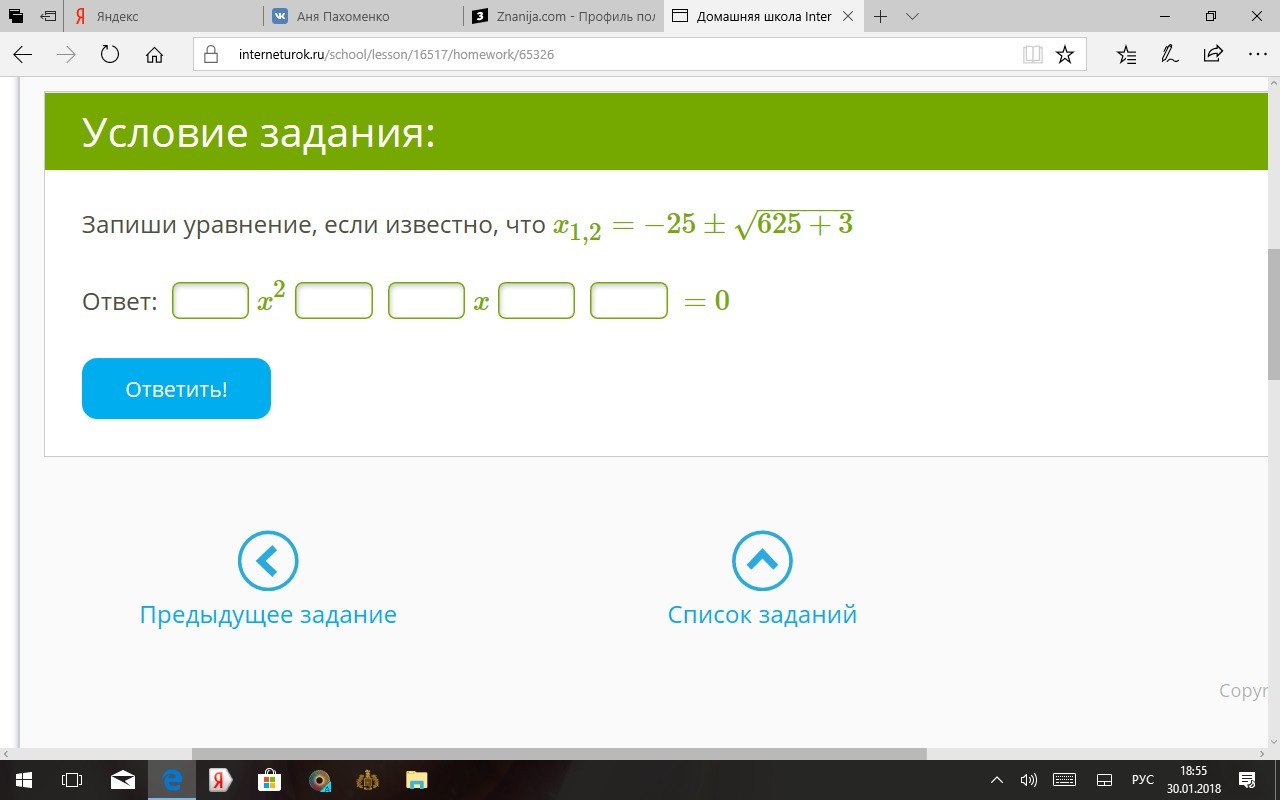
х₁ = -25-√(625+3)
х₂ = -25+√(625+3)
1) x₁+x₂ = -( -25-√(625+3)-25+√(625+3)) = - (-50)=50
2) х₁ · х₂ = (-25-√(625+3))·(-25+√(625+3)) =
= (-25)² - (√(625+3))² =
= 625 - (625+3) =
= 625 - 625 - 3 = - 3
3) Получим искомое уравнение:
х² + 50х - 3 = 0
Ответ: 1х² + 50х - 3 = 0
Можно иначе:
х₁ = -25-√(625+3)
х₂ = -25+√(625+3)
(х-х₁)(х-х₂)=0
(х-(-25-√(625+3))·(х-(-25+√(625+3))=0
(х+25-√628)·(х+25+√628)=0
(х+25)² - √638² = 0
х² + 2·25·х + 25² - 628 = 0
х² + 50х + 625 - 628 = 0
х²+ 50х - 3 = 0
2 задача
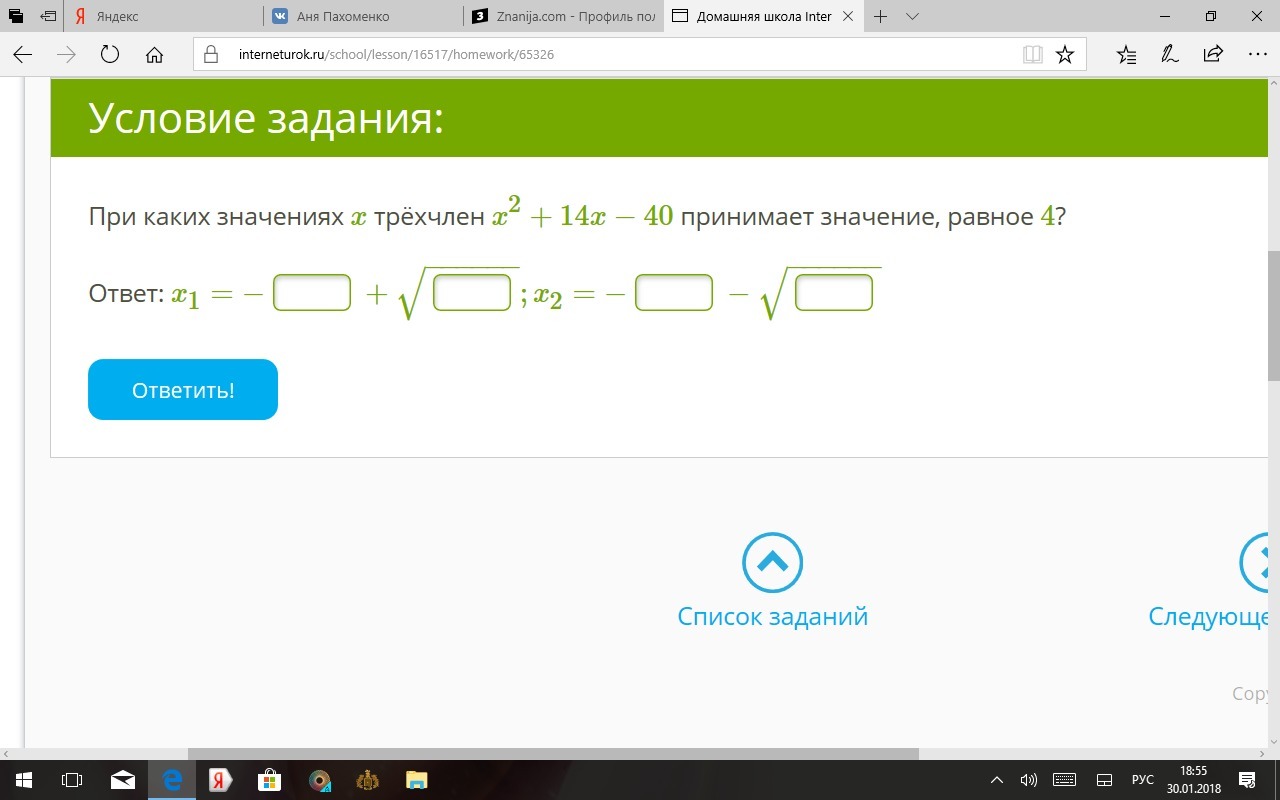
х²+14х-40=4
х²+14х-40-4=0
х²+14х-44=0
D=b²-4ac
D=14²-4·1·(-44)= 196+176=372
√D=√372=2√93
x₁=(-14-2√93)/2= -14-√93
x₂=(-14+2√93)/2= -14+√93
Ответ: x₁= -14 - √93
x₂= -14 + √93
ax² + bx +c =0 - общий вид квадратного уравнения
х² + (b/a)x + c/a = 0 -приведённый вид квадратного уравнения, для которого выполняется теорема Виета:
x₁+x₂= - b/а
x₁ · x₂= c/а
х₁ = -25-√(625+3)
х₂ = -25+√(625+3)
1) x₁+x₂ = -( -25-√(625+3)-25+√(625+3)) = - (-50)=50
2) х₁ · х₂ = (-25-√(625+3))·(-25+√(625+3)) =
= (-25)² - (√(625+3))² =
= 625 - (625+3) =
= 625 - 625 - 3 = - 3
3) Получим искомое уравнение:
х² + 50х - 3 = 0
Ответ: 1х² + 50х - 3 = 0
Можно иначе:
х₁ = -25-√(625+3)
х₂ = -25+√(625+3)
(х-х₁)(х-х₂)=0
(х-(-25-√(625+3))·(х-(-25+√(625+3))=0
(х+25-√628)·(х+25+√628)=0
(х+25)² - √638² = 0
х² + 2·25·х + 25² - 628 = 0
х² + 50х + 625 - 628 = 0
х²+ 50х - 3 = 0
2 задача
х²+14х-40=4
х²+14х-40-4=0
х²+14х-44=0
D=b²-4ac
D=14²-4·1·(-44)= 196+176=372
√D=√372=2√93
x₁=(-14-2√93)/2= -14-√93
x₂=(-14+2√93)/2= -14+√93
Ответ: x₁= -14 - √93
x₂= -14 + √93
Автор ответа:
0
огромное Спасибо!)
Похожие вопросы
Предмет: Математика,
автор: morozovamarija2010
Предмет: Английский язык,
автор: kosharnazlata5
Предмет: Литература,
автор: gubenkovzhenya
Предмет: Математика,
автор: katyamaks16
Предмет: Математика,
автор: ника7787