Предмет: Алгебра,
автор: NatashaS5E5
Помогите, пожалуйста!
Приложения:
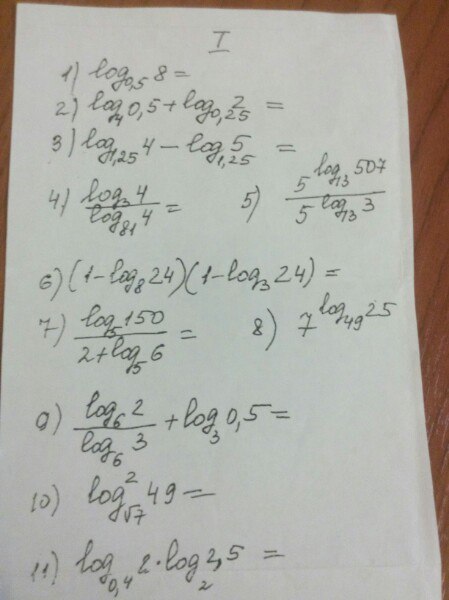
Ответы
Автор ответа:
0
Автор ответа:
0
Спасибо Вам большое!!!!))
Автор ответа:
0
а можно еще 6?
Похожие вопросы
Предмет: История,
автор: liko5788
Предмет: Английский язык,
автор: kakaha73
Предмет: Українська мова,
автор: ugtcuutcyxoy4433
Предмет: Геометрия,
автор: Аноним
Предмет: Биология,
автор: Аноним