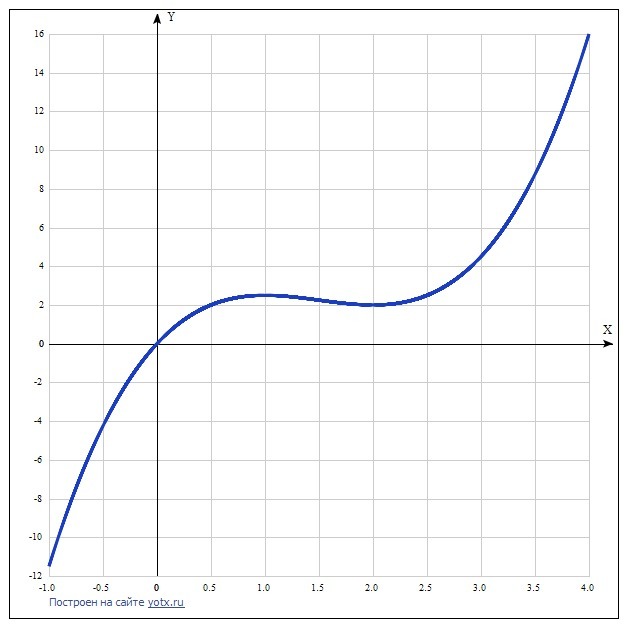
Исследовать функцию y=x³-4,5x²+6x
Ответы
Дана функция y=x³-4,5x²+6x
1. Область определения функции - вся числовая ось.
2. Функция f (x) = x³-4,5x²+6x непрерывна на всей области
определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
График четной функции симметричен относительно оси ОУ, а нечетной — относительно начала координат О.
f(–x) = (–x)³–4,5(–x)²+6(-х) = –x³- 4,5x²- 6х ≠ f(-x),
f(–x) = (–x)³–4,5(–x)²+(-х) = –(x³+4,5x²+6х) ≠ –f(x)
Функция не является ни четной, ни нечетной. Функция
непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0,
4x³–4,5x² + 6х = 0,
x(4x²–4,5x + 6) = 0.
Один корень уравнения равен х = 0.
Второй множитель - квадратный трёхчлен. Его дискриминант равен
D=(-4.5)^2-4*1*6=20.25-4*6=20.25-24=-3.75;
Дискриминант меньше 0, уравнение не имеет корней.
Значит, имеем 1 точку пересечения с осью Ох: х = 0.
Она же является точкой пересечения с осью Оу: у = 0
Точка (0; 0).
5. Промежутки монотонности и точки экстремума:
Находим производную: y' = 3x²-9x+6 и приравниваем нулю.
y'=0 ⇒ 3x²-9x+6 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант: D=(-9)^2-4*3*6=81-4*3*6=81-12*6=81-72=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√9-(-9))/(2*3)=(3-(-9))/(2*3)=(3+9)/(2*3)=12/(2*3)=12/6=2;
x_2=(-√9-(-9))/(2*3)=(-3-(-9))/(2*3)=(-3+9)/(2*3)=6/(2*3)=6/6=1.
Имеем две критические точки: х = 1 и х = 2 и три промежутка монотонности функции (-∞; 1), (1; 2) и (2; +∞).
На промежутках находим знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = 0 1 1,5 2 3
y' = 6 0 -0,75 0 6 .
Отрезки (-∞; 0) и (2; +∞) функция возрастает,
отрезок (1; 2) функция убывает,
7. Вычисление второй производной:
f '(x) = 3x² - 9x + 6. f ''(x) = 6x - 9.
y''= 0, 6x–9 = 0, x = 9/6 =3/2.
Точка ((3/2); 2,2963)
8. Промежутки выпуклости и точки перегиба:
отрезок (-∞; (3/2) график функции выпуклый вверх,
точка перегиба х = 3/2,
отрезок ((3/2); +∞) график функции выпуклый вниз.
9. Таблица точек:
x y
-1.0 -11.5
-0.5 -4.2
0 0
0.5 2
1.0 2.5
1.5 2.3
2.0 2
2.5 2.5
3.0 4.5
3.5 8.8
4.0 16
10. Искомый график функции в приложении.