Предмет: Геометрия,
автор: afanasevanatal
много баллов
ПОМОГИТЕ
Приложения:
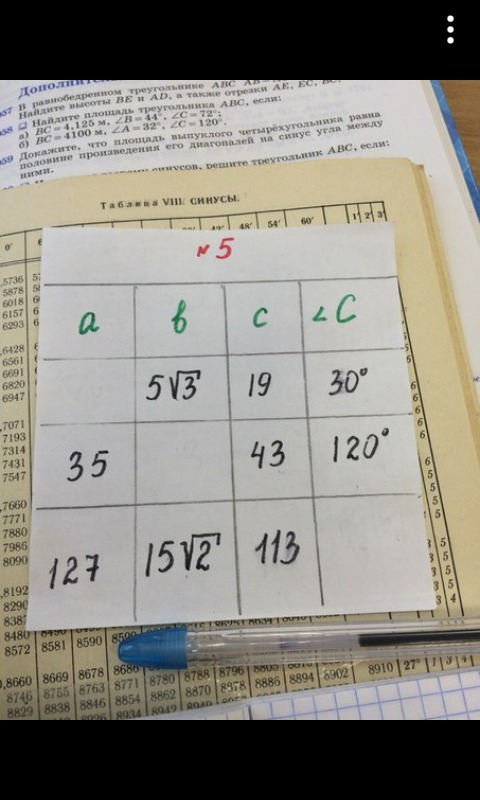
Ответы
Автор ответа:
0
1)
применим теорему косинусов:

Ответ: a=26
2)
еще раз теорема косинусов:

Ответ: b=13
3)
теорема косинусов:

Ответ: C=45°
применим теорему косинусов:
Ответ: a=26
2)
еще раз теорема косинусов:
Ответ: b=13
3)
теорема косинусов:
Ответ: C=45°
Похожие вопросы
Предмет: Математика,
автор: ninelebax
Предмет: Математика,
автор: arab2280
Предмет: Алгебра,
автор: mamedklycewamalika
Предмет: Математика,
автор: jdjdjdhdhdhdhdh
Предмет: Математика,
автор: 5Antony5