Предмет: Геометрия,
автор: darinkaklass511
помогите решить номер 8
Приложения:

Ответы
Автор ответа:
0
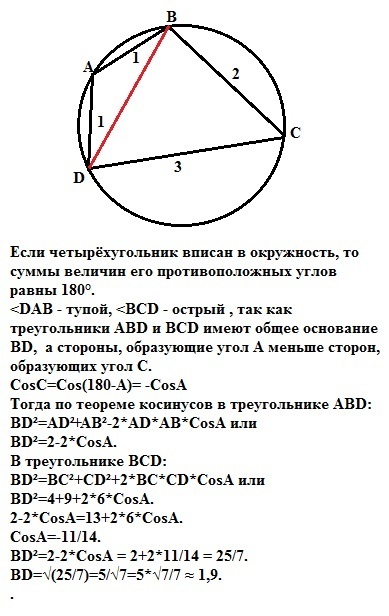
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
<DAB - тупой, <BCD - острый , так как треугольники АВD и ВСD имеют общее основание BD, а стороны, образующие угол А меньше сторон, образующих угол С.
CosC=Cos(180-A)= -CosA
Тогда по теореме косинусов в треугольнике ABD:
BD²=AD²+AB²-2*AD*AB*CosA или
BD²=2-2*CosA.
В треугольнике ВСD:
BD²=BC²+CD²+2*BC*CD*CosA или
BD²=4+9+2*6*CosA.
2-2*CosA=13+2*6*CosA.
CosA=-11/14.
BD²=2-2*CosA = 2+2*11/14 = 25/7.
BD=√(25/7)=5/√7=5*√7/7 ≈ 1,9.
<DAB - тупой, <BCD - острый , так как треугольники АВD и ВСD имеют общее основание BD, а стороны, образующие угол А меньше сторон, образующих угол С.
CosC=Cos(180-A)= -CosA
Тогда по теореме косинусов в треугольнике ABD:
BD²=AD²+AB²-2*AD*AB*CosA или
BD²=2-2*CosA.
В треугольнике ВСD:
BD²=BC²+CD²+2*BC*CD*CosA или
BD²=4+9+2*6*CosA.
2-2*CosA=13+2*6*CosA.
CosA=-11/14.
BD²=2-2*CosA = 2+2*11/14 = 25/7.
BD=√(25/7)=5/√7=5*√7/7 ≈ 1,9.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sendzucunade33
Предмет: Английский язык,
автор: abramovstepan32
Предмет: Информатика,
автор: GazDer
Предмет: Математика,
автор: номер9страница20
Предмет: Математика,
автор: Матеиатика