Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, решить неравенство. Подробно.
Приложения:
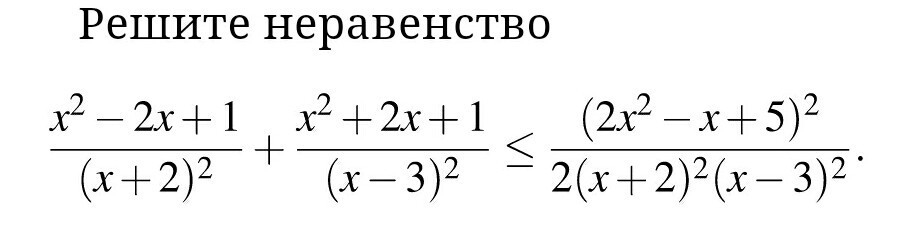
Ответы
Автор ответа:
0
учтем, что:

умножим обе части на (x+2)^2(x-3)^2 (так как данное выражение положительно и не равно 0 по одз) и свернем числители по формулам квадрат суммы и квадрат разности:

воспользуемся формулой квадрат трехчлена:

получим:


выражение (7x-1)^2 всегда больше или равно 0, поэтому:

решением неравенства является единственное значение x: x=1/7
Ответ:
умножим обе части на (x+2)^2(x-3)^2 (так как данное выражение положительно и не равно 0 по одз) и свернем числители по формулам квадрат суммы и квадрат разности:
воспользуемся формулой квадрат трехчлена:
получим:
выражение (7x-1)^2 всегда больше или равно 0, поэтому:
решением неравенства является единственное значение x: x=1/7
Ответ:
Похожие вопросы
Предмет: Геометрия,
автор: karinapark286
Предмет: Математика,
автор: mar12445mahina
Предмет: Алгебра,
автор: cimarnamarina2
Предмет: Математика,
автор: Аноним