Предмет: Алгебра,
автор: lollyguy
Решите логарифм, пожалуйста!
Приложения:
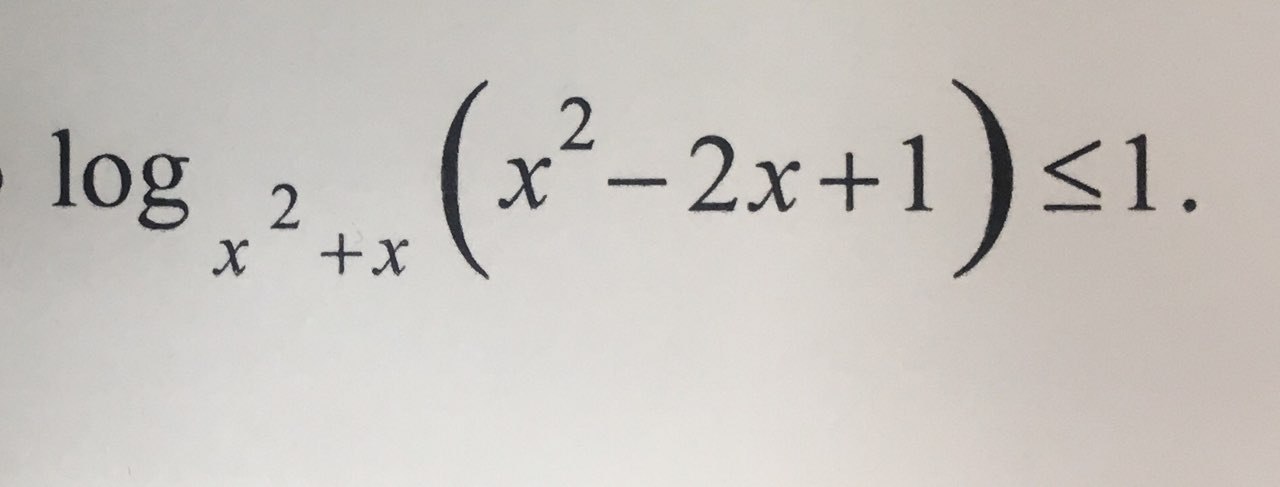
Ответы
Автор ответа:
0
Решаем методом замены множителей. Формула приведена.
Приложения:

Автор ответа:
0
если х=1, а это принадлежит ОДЗ, то подлогарифмическое выражение будет =0 а этого быть не должно
Автор ответа:
0
Х=1 сразу выколото,но я при окончательном решении эту точку поставила левее корня, а надо правее. Поэтому ответ : (-корень;-1)и (корень;1)и (1;бесконечность)
Автор ответа:
0
log(x²+x)(x-1)²≤1
{x-1≠0⇒x≠1
{x(x+1)>0⇒x<-1 U x>0
{x²+x≠1⇒x²+x-1≠0⇒x≠(-1-√5)/2 U x≠(-1+≠5)/2
x∈(-∞;(-1-√5)/2) U ((-1-√5)/2;-1) U (0;(√5-1)/2) U ((√5-1)/2;1) U (1;∞)
1)x∈(-∞;(-1-√5)/2) U ((√5-1)/2;1) U (1;∞) основание больше 1
(x-1)²≤x²+x
x²-2x+1-x²-x≤0
3x≥1
x≥1/3
x∈((√5-1)/2;1) U (1;∞)
2)x∈((-1-√5)/2;-1) U (0;(√5-1)/2) основание меньше 1
x≤1/3
x∈((-1-√5)/2;-1) U (0;1/3]
Ответ x∈((-1-√5)/2;-1) U (0;1/3] U ((√5-1)/2;1) U (1;∞)
{x-1≠0⇒x≠1
{x(x+1)>0⇒x<-1 U x>0
{x²+x≠1⇒x²+x-1≠0⇒x≠(-1-√5)/2 U x≠(-1+≠5)/2
x∈(-∞;(-1-√5)/2) U ((-1-√5)/2;-1) U (0;(√5-1)/2) U ((√5-1)/2;1) U (1;∞)
1)x∈(-∞;(-1-√5)/2) U ((√5-1)/2;1) U (1;∞) основание больше 1
(x-1)²≤x²+x
x²-2x+1-x²-x≤0
3x≥1
x≥1/3
x∈((√5-1)/2;1) U (1;∞)
2)x∈((-1-√5)/2;-1) U (0;(√5-1)/2) основание меньше 1
x≤1/3
x∈((-1-√5)/2;-1) U (0;1/3]
Ответ x∈((-1-√5)/2;-1) U (0;1/3] U ((√5-1)/2;1) U (1;∞)
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: xdpka
Предмет: География,
автор: pdpdpdp93
Предмет: Математика,
автор: migro7558
Предмет: Математика,
автор: bogdanrisaew