Question

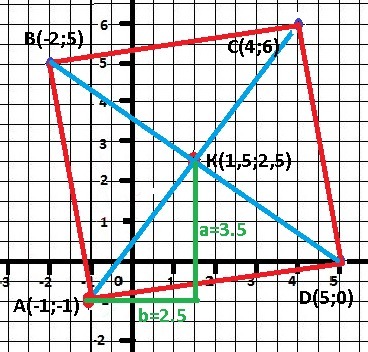
В квадрате ABCD задана вершина А (-1; -1) и точка пересечения диагоналей К (1,5; 2,5). Составить уравнения сторон и найти координаты остальных вершин.

Answer 1

Рисунок к задаче - в приложении.
ДАНО
Точки А(-1;-1 - вершина квадрата и 
К(1,5;2,5) - центр квадрата.
НАЙТИ
Вершины квадрата и другое по тексту вопроса.
РЕШЕНИЕ
Введем две промежуточные величины
а = Ку - Ау = 3,5 - разность координат по оси У.
b = Kx - Ax = 2.5 - разность координат по оси Х.
1) Находим координаты вершины С.
Словами - вершина С дальше от К на расстояние АК.
Находим координаты вершины С.
Сх =Кх + а = 1,5 + 2,5 = 4
Су = Ку +b = 2,5 + 3,5 = 6 
ОТВЕТ С(4;6) - координата вершины С.
2) Зная, что расстояние от центра квадрата до его вершин равны, то, используя значения постоянных - а и b, не трудно получить координаты двух других вершин.
Словами от точки К - b - налево, а - а - вверх и  наоборот.
В(-2;5) и D(5;0) - ОТВЕТ
3) Уравнения сторон - по формуле Y = k*x+b.
Расчет  для прямой АВ.
 Коэффициент k по формуле (для точек В и А)
k = ΔY/ΔX = (Ву-Ау)/(Вх-Ах) = (5 - (-1))/(-2 - (-1)) = - 6 - наклон 
Сдвиг по оси У по формуле (это другое b - сдвиг)
b =  Ву - k*Вx = 5 - (-6)*(-2) = 5 - 12 = -7  
Уравнение стороны ВА =  Y = - 6*x - 7. - ОТВЕТ
Остальное - самостоятельно.

Answer 2

Файл с рисунком не прикрепляется.