Предмет: Алгебра,
автор: EvansMari
Ребят, кто шарит в профильной математике? Помогите пожалуйста, кто может, с развернутым ответом
log5x/log5(x/625) – 4/log5x ≥ 12/(log25 x – log5x4)
Приложения:
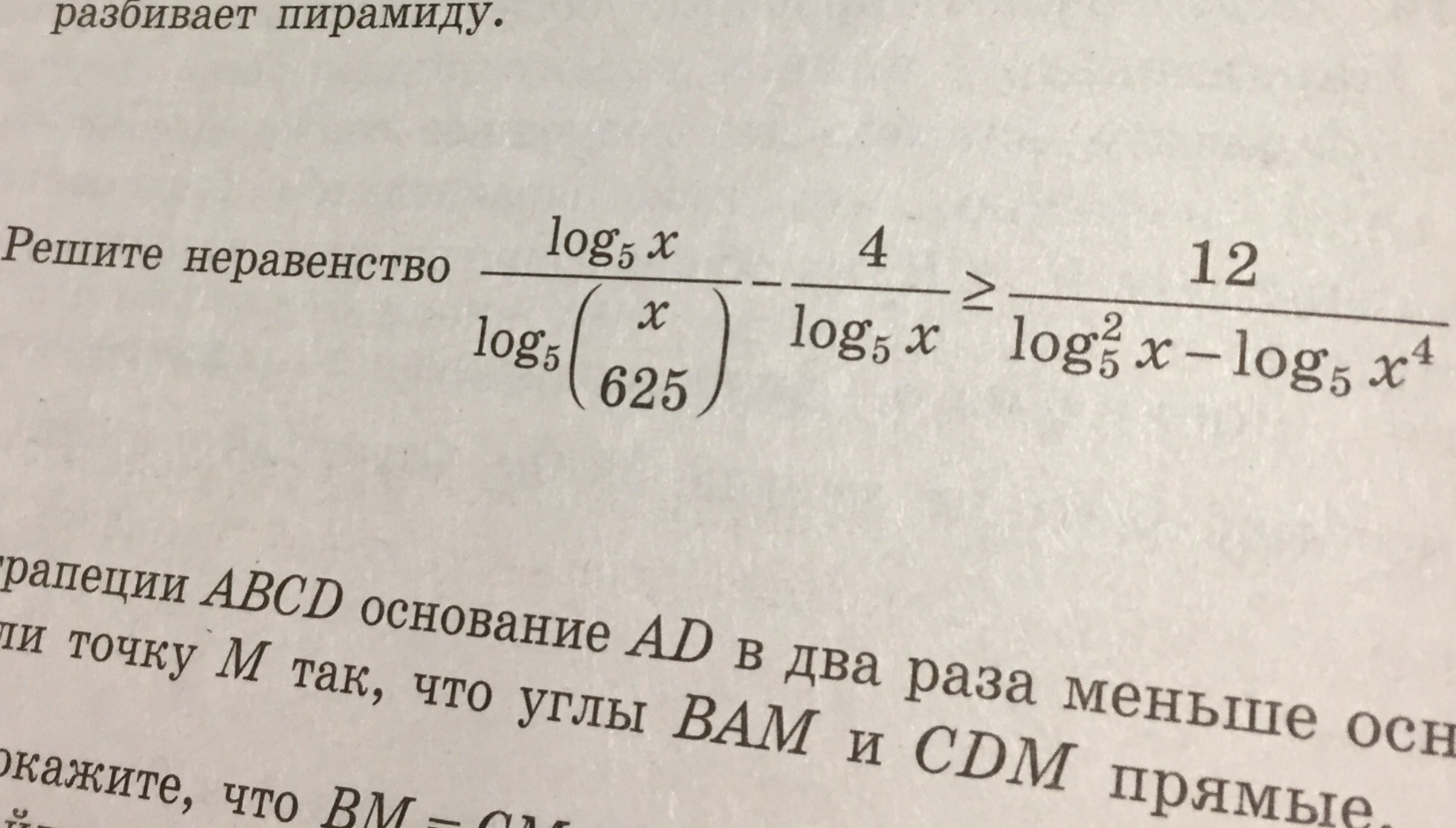
Ответы
Автор ответа:
0
1) сначала:
ОДЗ х >0
log₅ (x/625) = log₅x - log₅625 = log₅x -4
log₅x⁴ = 4log₅x
2) теперь log₅x = t и наше задание выглядит:
t/(t -4) -4/t ≥ 12/(t² -4t)
решаем. метод интервалов.
t/(t -4) -4/t - 12/(t² -4t) ≥ 0
(t² -4t -16 -12)/(t² -4t) ≥ 0
(t² -4t -28)/(t² - 4t) ≥ 0
Ищем нули числителя и знаменателя:
t² -4t -28= 0 t² - 4t =0
t = 2+-√32= 2 +- 4√2 t=0 t = 4
-∞ [2 -4√2] (0 ) (4) [2 + 4√2] +∞
+ - - - + знаки числителя
+ + - + + знаки знаменат.
IIIIIIIIIIIIIIIIII IIIIIIIIIIIIIII IIIIIIIIIIIIIIIII'это решение нер-ва
Теперь вернёмся к нашей переменной:
t ≤ -2-4√2 0< t < 4 t ≥ 2 + 4√2
1-е неравенство к ОДЗ не подходит
решаем 2-е
0< t < 4
0 < log₅x < 4
1 < x < 625
ОДЗ х >0
log₅ (x/625) = log₅x - log₅625 = log₅x -4
log₅x⁴ = 4log₅x
2) теперь log₅x = t и наше задание выглядит:
t/(t -4) -4/t ≥ 12/(t² -4t)
решаем. метод интервалов.
t/(t -4) -4/t - 12/(t² -4t) ≥ 0
(t² -4t -16 -12)/(t² -4t) ≥ 0
(t² -4t -28)/(t² - 4t) ≥ 0
Ищем нули числителя и знаменателя:
t² -4t -28= 0 t² - 4t =0
t = 2+-√32= 2 +- 4√2 t=0 t = 4
-∞ [2 -4√2] (0 ) (4) [2 + 4√2] +∞
+ - - - + знаки числителя
+ + - + + знаки знаменат.
IIIIIIIIIIIIIIIIII IIIIIIIIIIIIIII IIIIIIIIIIIIIIIII'это решение нер-ва
Теперь вернёмся к нашей переменной:
t ≤ -2-4√2 0< t < 4 t ≥ 2 + 4√2
1-е неравенство к ОДЗ не подходит
решаем 2-е
0< t < 4
0 < log₅x < 4
1 < x < 625
Автор ответа:
0
у меня же поучилось (0, 25) (625, + бесконечность) и я не понимаю откуда 1 и вырезанная точка 25
Автор ответа:
0
извини меня за комментарий начальный-а я поняла откуда
Автор ответа:
0
в знаменателе есть log(5)x не равен 0, а значит x не равен 5^0=1
Автор ответа:
0
ответ верный (0,1)U{25}U(625,+беск)
Автор ответа:
0
ОДЗ:x>0;log(5)x≠0;x≠1;
log(5)^2x≠log(5)x^4; log(5)x(log(5)x-4)≠0;log(5)x≠4;x≠625
обозначу log(5)x=y
(y^2-4(y-4))/(y(y-4))≥12/(y(y-4)); (y^2-4y+16-12)/(y(y-4))≥0
Дробь ≥0 если :надо рассматривать несколько случаев
а)числитель ≥0 и знаменатель >0
б)числитель ≤0 и знаменатель <0
а)y^2-4y+4=(y-2)^2 ≥0 при любых у
y(y-4)>0 при 1) y>0; y-4>0 и тогда общий ответ y>4
при 2)y<0;y-4<0 и тогда y<0
б)y^2-4y+4=(y-2)^2≤0 справедливо только при y=2
y(y-4)<0 при 1)y<0;y-4>0 и тогда общий ответ пуст
при 2)y>0;(y-4)<0 и тогда общий ответ y=2
Ответ по y: y>4; y<0;y=2
переходя к х и учитывая ОДЗ-получаем ответ
x=(0;1)U{25}U(625;+ беск)
log(5)^2x≠log(5)x^4; log(5)x(log(5)x-4)≠0;log(5)x≠4;x≠625
обозначу log(5)x=y
(y^2-4(y-4))/(y(y-4))≥12/(y(y-4)); (y^2-4y+16-12)/(y(y-4))≥0
Дробь ≥0 если :надо рассматривать несколько случаев
а)числитель ≥0 и знаменатель >0
б)числитель ≤0 и знаменатель <0
а)y^2-4y+4=(y-2)^2 ≥0 при любых у
y(y-4)>0 при 1) y>0; y-4>0 и тогда общий ответ y>4
при 2)y<0;y-4<0 и тогда y<0
б)y^2-4y+4=(y-2)^2≤0 справедливо только при y=2
y(y-4)<0 при 1)y<0;y-4>0 и тогда общий ответ пуст
при 2)y>0;(y-4)<0 и тогда общий ответ y=2
Ответ по y: y>4; y<0;y=2
переходя к х и учитывая ОДЗ-получаем ответ
x=(0;1)U{25}U(625;+ беск)
Похожие вопросы
Предмет: Английский язык,
автор: katredcat
Предмет: Математика,
автор: polina201146
Предмет: Математика,
автор: puhovaasona
Предмет: Математика,
автор: ольга413