Предмет: Математика,
автор: malenkiburatino
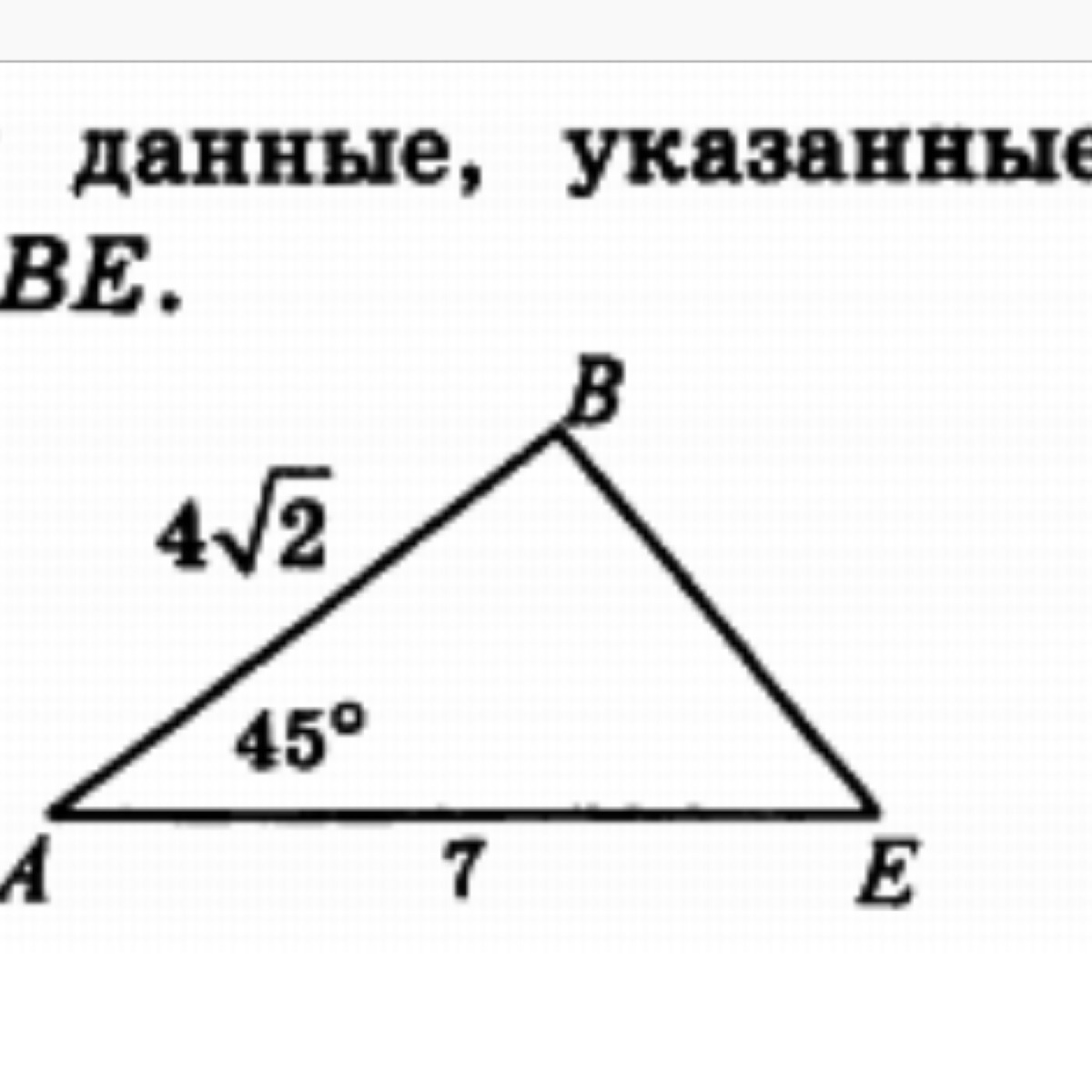
Используя данные, указанные на рисунке, найдите сторону бе
Приложения:
Ответы
Автор ответа:
0
Способ 1. Опустим перпендикуляр ВН на сторону АЕ. Треугольник АВН прямоугольный, угол А=45°, ВН=АВ•sin45°-4√2•√2/2=4. Сумма острых углов прямоугольного треугольника 90°, следовательно, угол АВН=45°. Два угла треугольника при АВ равны, - ∆ АВН равнобедренный, АН=ВН. Тогда в прямоугольном треугольнике ВЕН катет ЕН=АЕ-АН=7-4=3. Отношение катетов 3:4 указывает на то, что ∆ ВНЕ - египетский и ВЕ=5, или вычислив по т.Пифагора получим ВЕ=5.
Способ 2 По т. косинусов. ВЕ²=АВ²+АЕ²-2АВ•АЕ•cos45° Подставив известные значения и проведя вычисления, получим тот же резулльтат: ВЕ=5
Похожие вопросы
Предмет: Английский язык,
автор: dima9240pech
Предмет: Русский язык,
автор: asantemirov2010
Предмет: Биология,
автор: hhtghthaSD
Предмет: Математика,
автор: egor4ik112
Предмет: Математика,
автор: olesya172