Помогите, решить. Подробно.
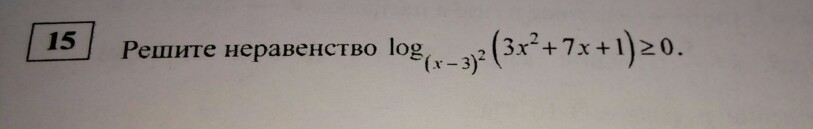
Ответы
ОДЗ:
Решаем первое неравенство:
Объединяем ОДЗ в одну систему:
Решаем исходное неравенство. Преобразуем исходный логарифм:
Вычтем из числителя и знаменателя по нулю:
И представим эти нули в виде логарифмов:
Учитывая возрастание функции на всей
области определения, можно перейти к неравенству:
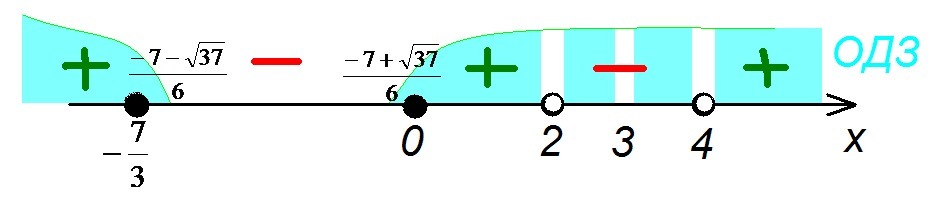
Неравенство решаем методом интервалов (картинка):
Отчетливо видно, что второе ОДЗ выполняется: числа 2, 3, 4 в решение не попали. Проверить первое условие можно с помощью приближенных вычисления или более точными методами.
Оценим значение выражения
То есть число расположено
правее числа
. Рассуждая аналогично, можно понять,
что число
расположено левее нуля. Таким
образом, наложение ОДЗ (картинка) никоим образом не меняет множество найденных
решений.
Ответ: