Предмет: Алгебра,
автор: BJIADA
Решите данное неравенство
Приложения:
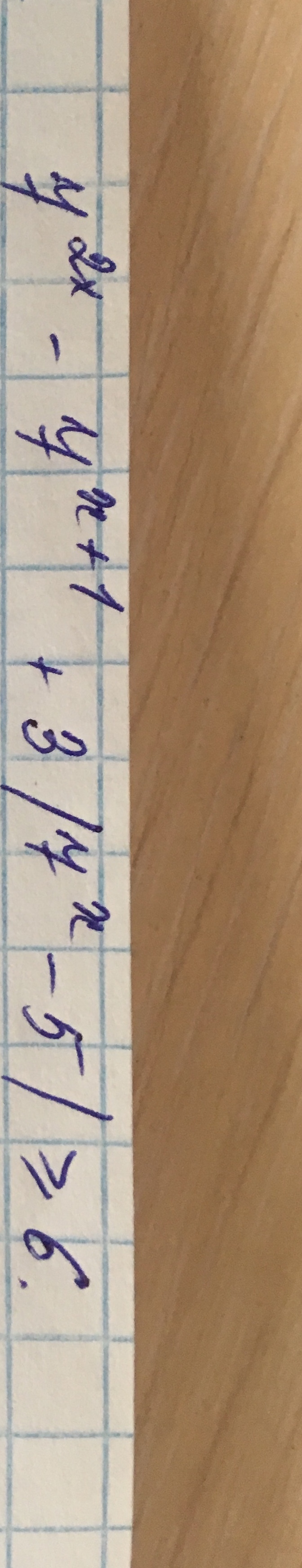
Ответы
Автор ответа:
0
делаем замену:

тогда:

раскрываем модуль:

решаем методом интервалов(см. приложение 1)
![y in (-infty;-3]cup [7;+infty) y in (-infty;-3]cup [7;+infty)](https://tex.z-dn.net/?f=y+in+%28-infty%3B-3%5Dcup+%5B7%3B%2Binfty%29)
пересекаем с
![x in ((-infty;-3]cup [7;+infty))cap (0;+infty)=[7;+infty) x in ((-infty;-3]cup [7;+infty))cap (0;+infty)=[7;+infty)](https://tex.z-dn.net/?f=x+in+%28%28-infty%3B-3%5Dcup+%5B7%3B%2Binfty%29%29cap+%280%3B%2Binfty%29%3D%5B7%3B%2Binfty%29)
![2)y^2-7y-3(y-5) geq 6, y leq 5; y in (-infty;5]
\y in (0;+infty)cap (-infty;5]=(0;5]
\y^2-7y-3y+15 geq 6
\y^2-10y+9 geq 0
\D=100-36=64=8^2
\y_1= frac{10+8}{2} =9
\y_2= frac{10-8}{2}=1
\(y-9)(y-1) geq 0
2)y^2-7y-3(y-5) geq 6, y leq 5; y in (-infty;5]
\y in (0;+infty)cap (-infty;5]=(0;5]
\y^2-7y-3y+15 geq 6
\y^2-10y+9 geq 0
\D=100-36=64=8^2
\y_1= frac{10+8}{2} =9
\y_2= frac{10-8}{2}=1
\(y-9)(y-1) geq 0](https://tex.z-dn.net/?f=2%29y%5E2-7y-3%28y-5%29+geq+6%2C+y+leq++5%3B+y+in+%28-infty%3B5%5D%0A%5Cy+in+%280%3B%2Binfty%29cap+%28-infty%3B5%5D%3D%280%3B5%5D%0A%5Cy%5E2-7y-3y%2B15+geq+++6%0A%5Cy%5E2-10y%2B9+geq++0%0A%5CD%3D100-36%3D64%3D8%5E2%0A%5Cy_1%3D+frac%7B10%2B8%7D%7B2%7D+%3D9%0A%5Cy_2%3D+frac%7B10-8%7D%7B2%7D%3D1%0A%5C%28y-9%29%28y-1%29+++geq+0%0A)
решаем методом интервалов(см. приложение 2)
![y in (-infty;1]cup [9;+infty) y in (-infty;1]cup [9;+infty)](https://tex.z-dn.net/?f=y+in+%28-infty%3B1%5Dcup+%5B9%3B%2Binfty%29)
пересекаем с![(0;5] (0;5]](https://tex.z-dn.net/?f=%280%3B5%5D)
![y in ((-infty;1]cup [9;+infty))cap (0;5]=(0;1] y in ((-infty;1]cup [9;+infty))cap (0;5]=(0;1]](https://tex.z-dn.net/?f=y+in+%28%28-infty%3B1%5Dcup+%5B9%3B%2Binfty%29%29cap+%280%3B5%5D%3D%280%3B1%5D)
объединяем получившееся множества:
![y in (0;1] cup [7;+infty) y in (0;1] cup [7;+infty)](https://tex.z-dn.net/?f=y+in+%280%3B1%5D+cup+%5B7%3B%2Binfty%29)
делаем обратную замену:
![left[begin{array}{ccc}0 textless 7^x leq 1 \7^x geq 7end{array}right. Rightarrow left[begin{array}{ccc} left { {{7^x textgreater 0} atop {7^x leq 1 }} right. \x geq 1end{array}right. Rightarrow left[begin{array}{ccc}left { {{x in R} atop {x leq 0 }} right. \x in [1;+infty)end{array}right. Rightarrow left[begin{array}{ccc}x in (-infty;0]\x in [1;+infty)end{array}right.
\x in (-infty;0] cup [1;+infty)
left[begin{array}{ccc}0 textless 7^x leq 1 \7^x geq 7end{array}right. Rightarrow left[begin{array}{ccc} left { {{7^x textgreater 0} atop {7^x leq 1 }} right. \x geq 1end{array}right. Rightarrow left[begin{array}{ccc}left { {{x in R} atop {x leq 0 }} right. \x in [1;+infty)end{array}right. Rightarrow left[begin{array}{ccc}x in (-infty;0]\x in [1;+infty)end{array}right.
\x in (-infty;0] cup [1;+infty)](https://tex.z-dn.net/?f=++left%5Bbegin%7Barray%7D%7Bccc%7D0+textless++7%5Ex+leq++1+%5C7%5Ex+geq+7end%7Barray%7Dright.+Rightarrow+++left%5Bbegin%7Barray%7D%7Bccc%7D++left+%7B+%7B%7B7%5Ex+textgreater++0%7D+atop+%7B7%5Ex+leq+1+%7D%7D+right.++%5Cx++geq+1end%7Barray%7Dright.+Rightarrow++++left%5Bbegin%7Barray%7D%7Bccc%7Dleft+%7B+%7B%7Bx+in+R%7D+atop+%7Bx+leq+0+%7D%7D+right.+%5Cx+in+%5B1%3B%2Binfty%29end%7Barray%7Dright.+Rightarrow+++left%5Bbegin%7Barray%7D%7Bccc%7Dx+in+%28-infty%3B0%5D%5Cx+in+%5B1%3B%2Binfty%29end%7Barray%7Dright.%0A%5Cx+in+%28-infty%3B0%5D+cup+%5B1%3B%2Binfty%29%0A%0A)
Ответ:![x in (-infty;0] cup [1;+infty) x in (-infty;0] cup [1;+infty)](https://tex.z-dn.net/?f=x+in+%28-infty%3B0%5D+cup+%5B1%3B%2Binfty%29)
тогда:
раскрываем модуль:
решаем методом интервалов(см. приложение 1)
пересекаем с
решаем методом интервалов(см. приложение 2)
пересекаем с
объединяем получившееся множества:
делаем обратную замену:
Ответ:
Приложения:

Похожие вопросы
Предмет: Математика,
автор: PotatoArtist6
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Arolov
Предмет: Математика,
автор: АЛЕКС20041