Question

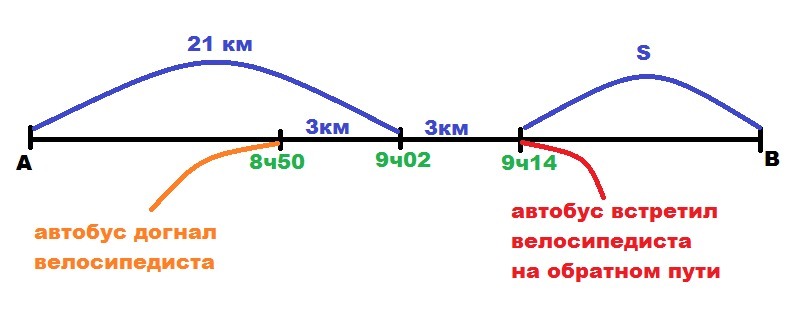
Автобус отправляется из пункта А в пункт Б и после 6 минут стоянки в Б возвращается в А, двигаясь в обоих направлениях с одно и той же постоянной скоростью. На пути из пункта А в Б в 8часов 50 минут автобус догоняет велосипедиста, который движется из А в Б с постоянной скоростью 15 км/ч. В 9 часов 02 минуты велосипедист находится на расстоянии 21 км от А. Автобус возвращаясь из Б в А после останов

Answer 1

Скорость велосипедиста 15 км/ч. 
12 минут = 12/60 ч = 0,2 ч
24 минуты = 0,2 * 2 = 0,4 ч

За 12 минут пути с 8:50  до  9:02 велосипедист  проехал
15 * 0,2 = 3 км
⇒ Когда автобус догнал велосипедиста в 8.50, расстояние до пункта А было      21 - 3 = 18 км.

С 8:50 (первая встреча с автобусом) до 9:14 (вторая встреча с автобусом) велосипедист проехал  15*0,4 = 6 км

Пусть S - расстояние от места второй встречи автобуса с велосипедистом до пункта В 
С 8:50 (первая встреча с велосипедистом)  до 9:14 (вторая встреча с велосипедистом) автобус проехал расстояние
6 + S + S = 2S + 6 км, затратив на этот путь время 
24 мин - 6 мин = 0,4 ч - 0,1 ч = 0,3 часа
Тогда скорость автобуса
$v = frac{2S + 6}{0,3} = frac{20S+ 60}{3}$

После второй встречи автобусу осталось проехать расстояние 
18 + 6 = 24 км до пункта А
Велосипедисту осталось проехать расстояние S до пункта В.
Прибыли они одновременно
$frac{24}{frac{20S+ 60}{3}} = frac{S}{15} \ \ frac{24*3}{20S+60} = frac{S}{15}$
Сократить слева на 4 и все домножить на 5
$frac{18}{S+3} = frac{S}{3} \ \ S(S+3) = 18*3 \ \ S^2+3S-54=0 \ \ D = 9+4*54 = 225 = 15^2 \ \ S= frac{-3 + 15}{2} = 6$

Скорость автобуса
$v =frac{20S+ 60}{3}= frac{20*6+60}{3} =60$ км/ч
Расстояние 18 км до места первой встречи автобус прошел за
$frac{18}{60}$ часа, т.е. за 18 минут

Отнять от времени первой встречи 18 минут
8 ч 50 мин - 18 мин = 8 ч 32 мин

Автобус отправился из пункта А в 8 часов 32 минуты