Предмет: Математика,
автор: zh96
1. Вычислить значения частных производных f’x (M0), f’y (M0), f’z (M0) для данной функции f (x,y,z) в точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.
2. Вычислить значение производной сложной функции u=u(x,y), где x=x(t), y=y(t), при t=t0 с точностью до двух знаков после запятой.
Приложения:
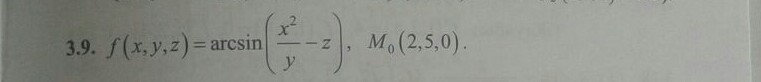
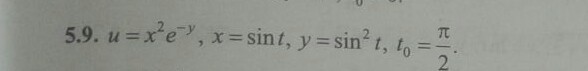
Ответы
Автор ответа:
0
1)







2)





2)
Автор ответа:
0
я еще раз перепроверил через калькулятор, получаются те же числа, которые отличны от ваших
Автор ответа:
0
но в общем, если у вас другие ответы, то я задачу неправильно решил, а как иначе ее решать - понятия не имею
Автор ответа:
0
Ладно тогда, спасибо вам.
Автор ответа:
0
Просто ответы так написаны в книге
Автор ответа:
0
еще раз спасибо
Похожие вопросы
Предмет: Математика,
автор: daniil2100bondarenko
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: LiZaP707465
Предмет: Музыка,
автор: Mibk
Предмет: Математика,
автор: mavrodililya