Предмет: Математика,
автор: zh96
Вычислить значения частных производных f’x (M0), f’y (M0), f’z (M0) для данной функции f (x,y,z) в точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.
Приложения:
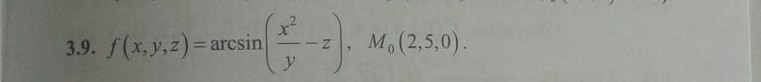
Ответы
Автор ответа:
0
3.9. Используем табличную производную арксинуса:

Используем производную сложной функции:

Когда берём частную производную по х, другие переменные (y и z) считаем константами. По остальным переменным аналогично.
В конце подставляем значения переменных в точке М0.



Используем производную сложной функции:
Когда берём частную производную по х, другие переменные (y и z) считаем константами. По остальным переменным аналогично.
В конце подставляем значения переменных в точке М0.
Автор ответа:
0
Спасибо большое за помощь, желаю вам успехов!!!
Похожие вопросы
Предмет: Литература,
автор: milaniasarkisan4
Предмет: Физика,
автор: cykingnom
Предмет: Алгебра,
автор: kovalevaelena81
Предмет: Математика,
автор: sabr5368
Предмет: Математика,
автор: shiralizade22