Предмет: Математика,
автор: zh96
Вычислить значение производной сложной функции u=u(x,y), где x=x(t), y=y(t), при t=t0 с точностью до двух знаков после запятой:
Приложения:
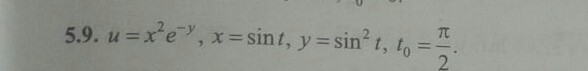
Ответы
Автор ответа:
0
5.9.

Автор ответа:
0
https://znanija.com/task/27479232
Автор ответа:
0
Можете вы решить это
Автор ответа:
0
помогите, если не трудно
Похожие вопросы
Предмет: Русский язык,
автор: ooo000o0o0
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: mavullina
Предмет: Математика,
автор: 02OLGA02
Предмет: Химия,
автор: Мятушkа