Предмет: Математика,
автор: kseniafolzz
решите то,которое справа.
буду очень благодарна.
Приложения:

Ответы
Автор ответа:
0
Приложения:
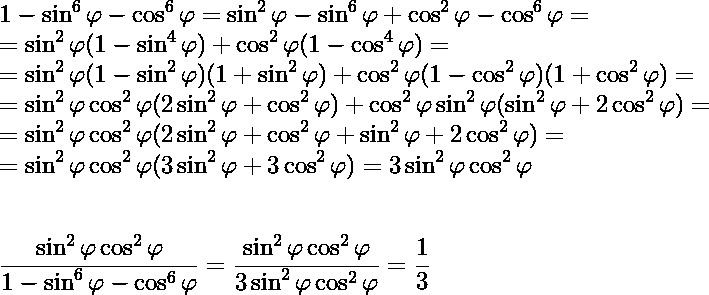
Автор ответа:
0
В предпоследней строке исправьте 2 на 3 (опечатка).
Автор ответа:
0
Уже давно исправлено, обновите страницу
Автор ответа:
0
о,а как вы пишите таким шрифтом?
Автор ответа:
0
Приложения:
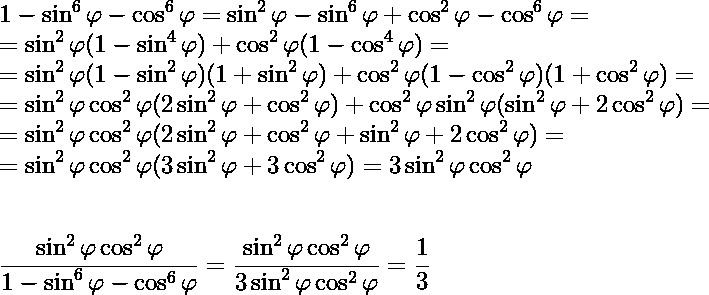
Автор ответа:
0
Можно было с числителем не заморачиваться =)
Автор ответа:
0
Хотя ваш вариант решения вообще от моего отличается. Респект =)
Похожие вопросы
Предмет: Физика,
автор: bouuntyyy
Предмет: История,
автор: bebra22800
Предмет: Английский язык,
автор: turik36191
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: pavsasha