Предмет: Математика,
автор: avva2
Окружности радиусов 2 и 3 внешним образом касаются друг друга в точке A. Их общая касательная, проходящая через точку A, пересекает две другие их общие касательные в точках B и C. Найти BC.
Ответы
Автор ответа:
0
9/Задание № 7:
Окружности радиусов 2 и 3 внешним образом касаются друг друга в точке A. Их общая касательная, проходящая через точку A, пересекает две другие их общие касательные в точках B и C. Найти BC.
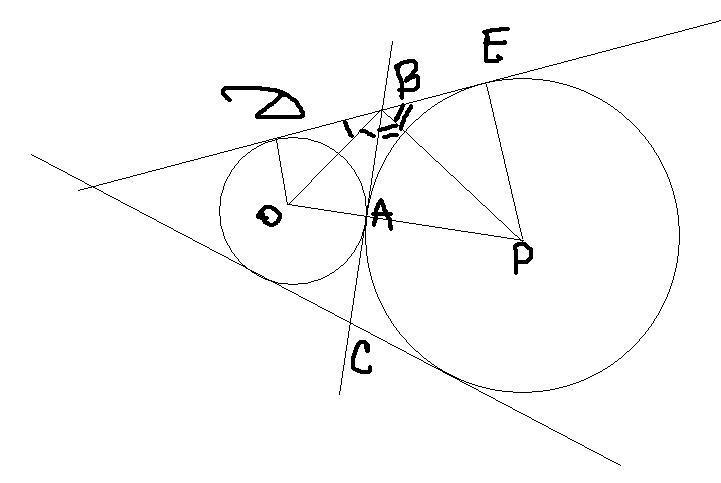
РЕШЕНИЕ: Треугольники ОВА и ОВD равны по 3 сторонам (общая, радиусы и отрезки касательных). Значит ВО - биссектриса угла АВD. По тем же причинам треугольники РВА и РВЕ равны, а ВР - биссектриса. Значит развернутый угол DBE содержит в себе два угла ОВР, так как содержит двойной набор углов составляющий углов. Значит ОВР=90 градусов, значит ВА - высота прямоугольного треугольника, равная ВА=√(АО*АР)=√(2*3)=√6
По такому сценарию определяем, что СА=√6, откуда ВС=2√6
ОТВЕТ: 2√6
Приложения:
Похожие вопросы
Предмет: История,
автор: zlata0212
Предмет: Другие предметы,
автор: alinakosev
Предмет: Русский язык,
автор: lykova21vk19
Предмет: Химия,
автор: ilfiriumi
Предмет: Физика,
автор: pokemondom