Предмет: Математика,
автор: troyansasha96
Найти производную, помогите, пожалуйста, в задании г) степень 1/х. Онлайн калькулятор не поможет, нужно полное решение.
Приложения:
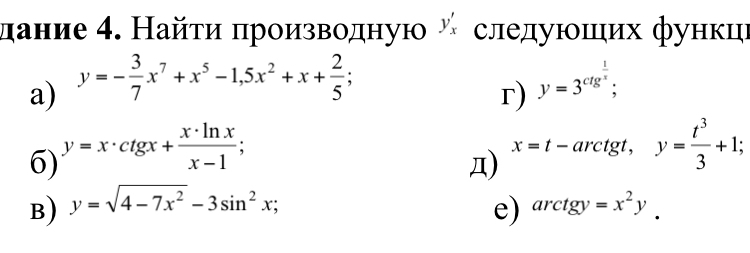
Ответы
Автор ответа:
0
Автор ответа:
0
Спасибо, огромное
Похожие вопросы
Предмет: Русский язык,
автор: zdravstvujtehoroso60
Предмет: Геометрия,
автор: talyana1
Предмет: Астрономия,
автор: MarchenkoOrest
Предмет: Физика,
автор: УЧЕНИК4577ц