Предмет: Математика,
автор: SkayTos
Помогите решить.
Алгоритмы
Приложения:
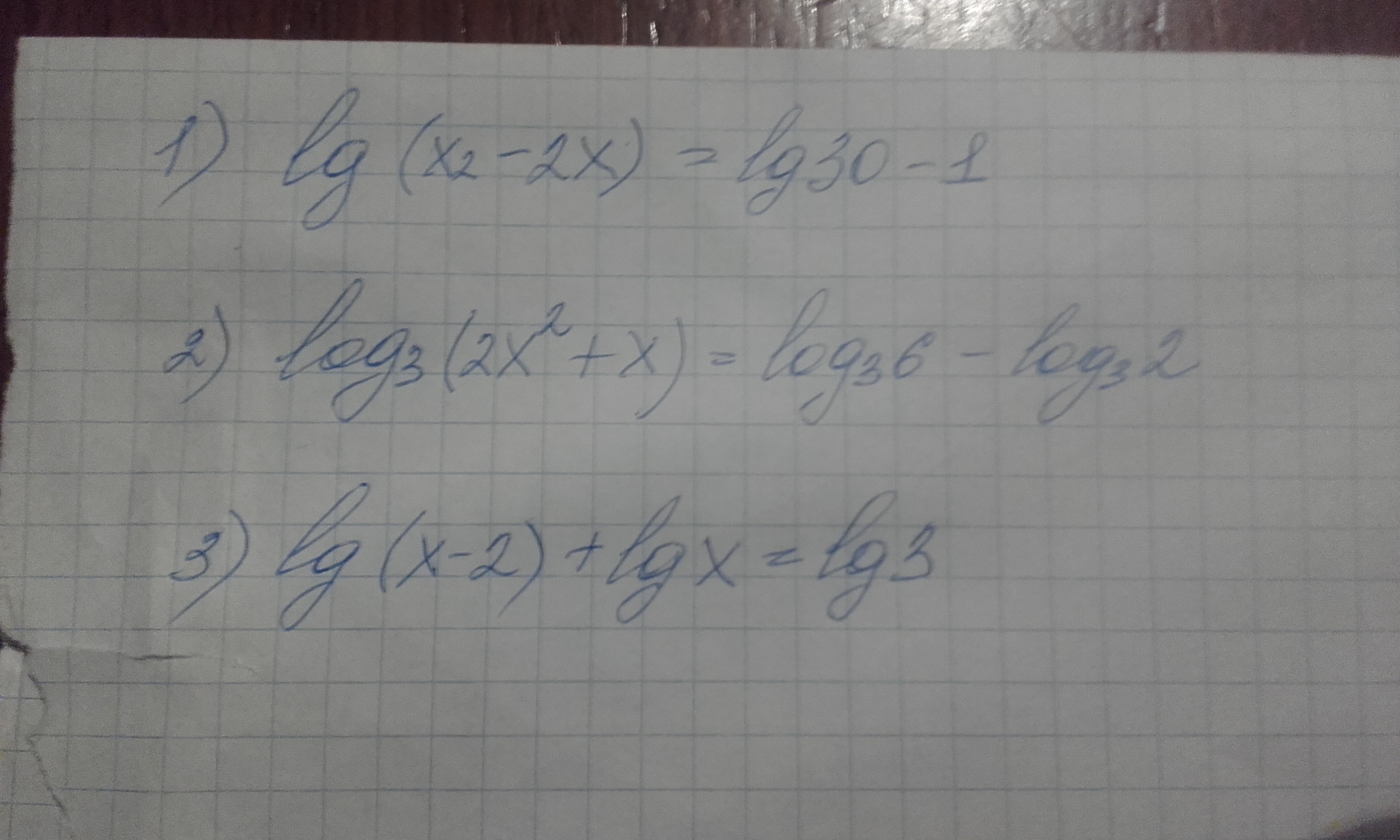
Ответы
Автор ответа:
0
1) [lg - десятичный логарифм, в которого основание 10]
Сделаем с 1 десятичный логарифм (чтобы основания были равны):
10¹= 10. Поэтому:
1= lg10.
Теперь упростим правую часть уравнения использовав свойство логарифмов при вычитании.
[ То есть если вычитаются логарифмы с одинаковыми основаниями, то в результате будет логарифм с этим основанием, а выражения поделятся]
То есть если вычитаются логарифмы с одинаковыми основаниями, то в результате будет логарифм с этим основанием, а выражения поделятся]
Получим уравнение:

Основания равны, значит можем приравнять выражения:

Получили квадратное уравнение типа: ax²+ bx+ c= 0.

Какой корень первый, а какой второй неважно.
2)

3) [ То есть, если сложиваются два логарифма с равными основаниями, то результатом будет логарифм с этим основанием, у выражении произведение выражений этих двоих логарифмов]
То есть, если сложиваются два логарифма с равными основаниями, то результатом будет логарифм с этим основанием, у выражении произведение выражений этих двоих логарифмов]

Сделаем с 1 десятичный логарифм (чтобы основания были равны):
10¹= 10. Поэтому:
1= lg10.
Теперь упростим правую часть уравнения использовав свойство логарифмов при вычитании.
[
Получим уравнение:
Основания равны, значит можем приравнять выражения:
Получили квадратное уравнение типа: ax²+ bx+ c= 0.
Какой корень первый, а какой второй неважно.
2)
3) [
Автор ответа:
0
Если что-то не ясно, спрашивай.
Автор ответа:
0
Хорошо спасибо большое
Автор ответа:
0
Пожалуйста. И это не алгоритмы, а логарифмы.
Похожие вопросы
Предмет: Українська мова,
автор: skubanika2008
Предмет: Химия,
автор: katiefeelfree
Предмет: Информатика,
автор: curlyrose
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: ЛиЛу1111