Question

Решите неравенство
3-Ιx-1Ι≥√x+2
(x+2) под корнем
Я решила, но не могу объединить в ответ.
В первой части у меня получился промежуток [-1;+∞) раскрывая модуль со знаком минус, во второй части у меня [2;4]

Answer 1

$3-|x-1| geq sqrt{x+2}$
возведем обе части в квадрат и составим систему:
$left{begin{array}{ccc}x+2 geq 0\(3-|x-1|)^2 geq x+2\3-|x-1| geq 0end{array}right$
решим каждое неравенство по отдельности:
$x+2 geq 0 \x geq -2 \x in [-2;+infty) \3-|x-1| geq 0 \|x-1| leq 3 \ left { {{x-1 leq 3} atop {x-1 geq -3}} right. Rightarrow left { {{x leq 4} atop {x geq -2}} right. Rightarrow x in [-2;4]$
$\(3-|x-1|)^2 geq x+2 \(x-1)^2+9-6|x-1| geq x+2 \x^2-2x+10-6|x-1| geq x+2 \x^2-3x+8 geq 6|x-1| \|6x-6| leq x^2-3x+8 \ left { {{6x-6 leq x^2-3x+8} atop {6x-6 geq -x^2+3x-8}} right. \ left { {{x^2-9x+14 geq 0} atop {-x^2-3x-2 leq 0}} right.$
решаем неравенства 2 системы  по отдельности:
$x^2-9x+14 geq 0 \D=81-56=25=5^2 \x_1= frac{9+5}{2} =7 \x_2= frac{9-5}{2} =2 \(x-7)(x-2) geq 0$
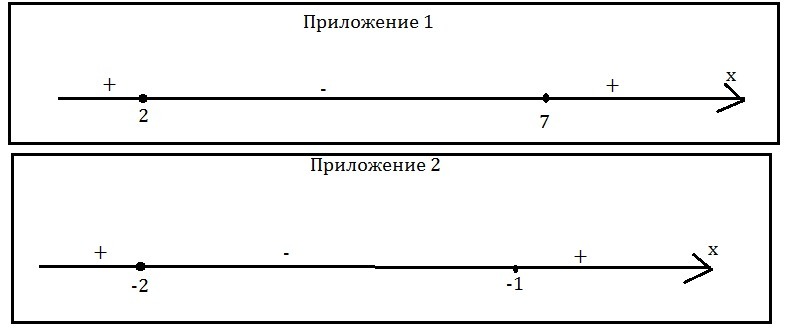
используем метод интервалов(см. приложение 1)
$x in (-infty;2]cup [7;+infty)$
$-x^2-3x-2 leq 0 \x^2+3x+2 geq 0 \D=9-8=1 \x_1= frac{-3+1}{2} =-1 \x_2= frac{-3-1}{2} =-2 \(x+1)(x+2) geq 0$
используем метод интервалов(см. приложение 2)
$x in (-infty;-2]cup [-1;+infty)$
пересекаем множества решений 2 системы:
$x in ((-infty;2]cup [7;+infty)) cap((-infty;-2]cup [-1;+infty))=\=(-infty;-2]cup [-1;2] cup [7;+infty)$
теперь пересекаем множества их решений 1 системы:
$x in [-2;4] cap ([-2;+infty)) cap ((-infty;-2]cup [-1;2] cup [7;+infty))=\=x in {-2} cup [-1;2]$
Ответ: $x in {-2} cup [-1;2]$